Podręcznik Grafika komputerowa i wizualizacja
Rozdział 8. MODELOWANIE OBIEKTÓW NATURALNYCH. MODELOWANIE FRAKTALNE I WOLUMETRYCZNE
8.4. "The Fractal Geometry of Nature"
Fraktale
stosuje się w grafice komputerowej przede wszystkim do modelowania kształtu
obiektów naturalnych wykazujących samopodobieństwo. Pozwalają kreować
nieregularne kształty roślin, (rzeźby) terenu, muszli, śniegu, efektów
atmosferycznych, itd., itp. Tytuł tego rozdziału został zaczerpnięty z książki
B.Mandelbrota [2]. Łączenie różnych metod modelowania z modelowaniem fraktalnym
daje możliwość uzyskania obiektów o kształtach zbliżonych lub bardzo podobnych
do obiektów naturalnych. Trudno jest jednak mówić o regułach takiego
modelowania czy projektowania obiektów, gdyż ze względu na różnorodność
kształtów występujących w naturze zasady modelowania są dobierane indywidualnie
do danego przypadku. Przykładem może być modelowanie krajobrazu. Fourier,
Fussel i Carpenter zaproponowali zastosowanie iteracyjnego podziału do
generowania fraktalnej góry. Jeśli podstawę góry będziemy dzielić
systematycznie na pół, to po odpowiedniej liczbie iteracji uzyskamy punkty o
zadanej dokładności. Wysokość dla każdego punktu podziału określa się na
podstawie wysokości punktów poprzedniego kroku iteracji oraz pewnej funkcji
zaburzenia, można też użyć parametrów terenu (mapy). W zależności od przyjętej
funkcji zaburzenia można w ten sposób otrzymać odpowiedni charakter zmian
wysokości (łagodne pagórki lub ostre szczyty).

Rys.8.9. „Wyspa Mandelbrota” przykład zastosowania technik
fraktalnych do modelowania
obiektów o wyglądzie zbliżonym do naturalnych.
Rysunek opracowany przez Prokofiev
i udostępniony w Wikimedii na licencji Creative Commons.
Można zaproponować prosty schemat generacji
rzeźby terenu (rys.8.10):
- Zdefiniować siatkę.
- W każdym węźle określić wysokość używając parametrów terenu (mapy) oraz/lub wartości losowych.
- Wygenerować nowe węzły – pośrednie (zagęścić siatkę) oraz określić ich wysokość (też mapa i/lub losowo).
- Sterując zakresem używanych wartości losowych określić kształt terenu (mniej lub bardziej płaski/pofałdowany).
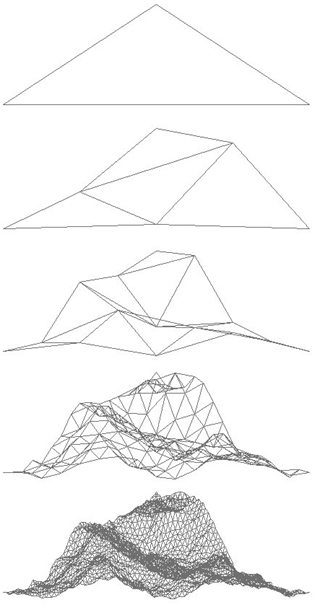
Rys.8.10. Kolejne etapy modelowania rzeźby terenu.
Z WIkimedii jako Public Domain.

Rys.8.11. Góry fraktalne. Rysunek wygenerowany programem
Terragen
i udostępniony w Wikimedii na licencji Creative Commons.
Klasyczne modelowanie roślin z wykorzystaniem L-Systemu daje możliwość zachowania w pełni samopodobieństwa modelowanego obiektu. Jest to związane z powtarzalnością iteracji i pełną symetrią generowanych kształtów. Jest to oczywiście podstawową zaletą tego mechanizmu. Jednak w sytuacji obiektów naturalnych takie zachowanie nie zawsze jest pożądane. Bogactwo kształtów obiektów naturalnych zawsze wykracza poza przyjęty i dowolnie zaawansowany schemat, poza pełną symetrię i poza całkowitą powtarzalność iteracji. Kształty roślin zachowują samopodobieństwo, jednak w rzeczywistości zależą od bardzo wielu czynników (także losowych) i nigdy nie są w stu procentach powtarzalne. W pełni symetryczne rośliny wyglądają po prostu zupełnie nienaturalnie (rys.8.12.a). Mechanizm iteracyjnego modelowania kształtu obiektów naturalnych wymaga „naturalnego” zaburzenia symetrii. Dobrym rozwiązaniem jest dodanie elementu losowego w trakcie generowania obiektu w ramach L-Systemu (rys.8.12.b).
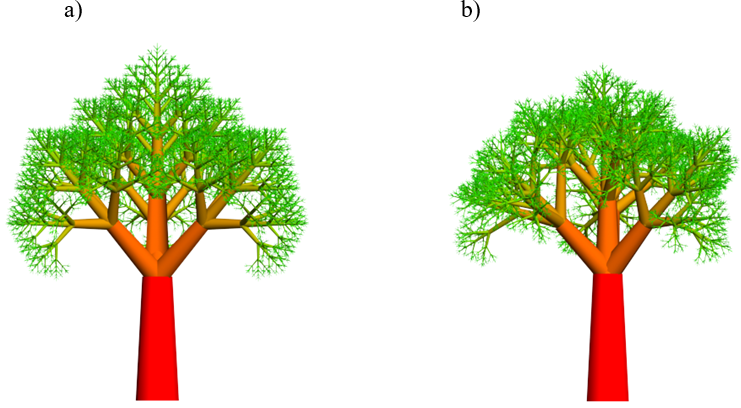
Rys.8.12. a) Nienaturalna symetria tradycyjnej generacji,
b) to samo drzewo po dodaniu wyboru losowego parametrów.
Rysunki M.Paterczyk © rysunki publikowane za zgodą Autora.

Rys.8.13. Obrazy liści i kory zastosowane do modelowania
dębu.
Rysunki M.Paterczyk © rysunki publikowane za zgodą Autora.
