Poprzedni

Rozdział 9. ELIMINACJA ELEMENTÓW ZASŁONIĘTYCH

9.9. Złożoność obliczeniowa algorytmów rozstrzygania widoczności

Twórcy algorytmów rozstrzygania widoczności starali się zawsze obniżyć złożoność obliczeniową tych algorytmów. Wielokrotnie były przeprowadzane analizy złożoności algorytmów zasłaniania.  Najciekawsze analizy złożoności algorytmów zasłaniania przeprowadzali:  Sutherland, Sproull, Schumacher w 1974,  Schmitt w 1981 i Fiume w 1989.

Wnioski jakie płyną z tych analiz:

  • Dla algorytmów w przestrzeni obiektu decydujące jest zastosowane sortowanie geometryczne. Dla typowych („niezłośliwych”) scen, można uzyskać złożoność postaci O(nlogn), gdzie n — liczba wielokątów.
  • Dla algorytmów pracujących w przestrzeni rzutu można uzyskać złożoność O(n), gdzie n — liczba wielokątów.

Analizy te pokazują, że nawet najtrudniejsze przypadki mogą zostać rozwiązane ze złożonością kwadratową. Z drugiej strony można się zastanawiać nad minimalną liczbą operacji, niezbędnych do rozwiązania problemu zasłaniania. W większości przypadków wyrafinowane algorytmy wyznaczają elementy zasłonięte ze złożonością O(nlogn), gdzie n jest miarą złożoności sceny (liczbą wielokątów lub krawędzi). Oczywiście dla algorytmów pracujących w przestrzeni rzutu (z precyzją obrazową) nie jest możliwe uzyskanie złożoności lepszej niż liniowa.

Można pokazać, że dla wybranych scen minimalna złożoność algorytmów pracujących w przestrzeni obiektu musi być rzędu kwadratowego. Wynika to z budowy sceny. Wyrafinowane algorytmy mogą w tym przypadku dać rozwiązanie gorsze niż kwadratowe. Przykłady takich „złośliwych” scen pokazuje rysunek 9.18. W obu przypadkach liczba różnych fragmentów wymagających analizy zasłaniania jest rzędu n2, jeśli n jest np. liczbą obiektów. Zatem algorytm eliminacji elementów zasłoniętych pracujący w przestrzeni obiektu nie może mieć niższej złożoności.


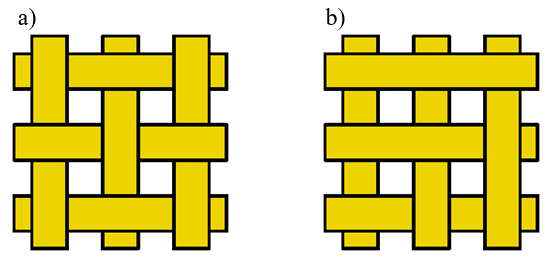
Rys.9.18. Przykłady sceny „złośliwej”.
a) Mata „plecionka” – obiekty nie są płaskie. 
b) Mata w wersji prostszej – obiekty są płaskie.


 


  Poprzedni