Podręcznik Grafika komputerowa i wizualizacja

Zadanie rysowania powierzchni będącej wykresem funkcji dwóch zmiennych jest jednym z częściej realizowanych zadań grafiki prezentacyjnej. Dodatkowo można zauważyć, że jest to dobry sposób uproszczonego rysowania rzeźby terenu.

Powierzchnia będąca wykresem funkcji z=f(x,y) należy do szczególnej klasy obiektów trójwymiarowych, dla której można pokazać uproszczony algorytm rozstrzygania widoczności.

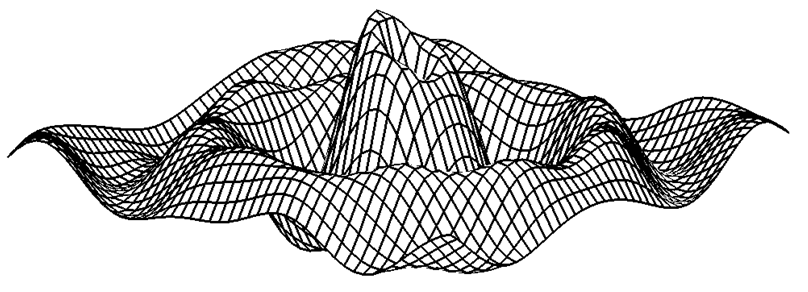
Rys.9.14. Wykres funkcji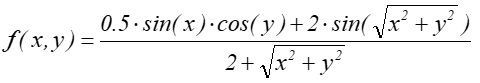

Można przyjąć, że dziedziną D funkcji dla rozpatrywanego fragmentu powierzchni jest prostokątem określonym przez zakresy zmiennych  [x_min,x_max] X [y_min,y_max]. Jeśli dziedzinę D podzielimy równomierną siatką za pomocą linii równoległych odpowiednio do osi x i osi y, to punkt  [x_i,y_j] będzie węzłem takiej siatki (dla 1 ≤ i ≤ NX oraz 1  ≤ j ≤ NY, gdzie NX, NY określają liczbę linii siatki dla każdej współrzędnej). Punkt [z_ij,x_i,y_j] dla z_ij=f(x_i,y_j) jest węzłem siatki rozpiętej na powierzchni będącej wykresem punkcji. Taki przykład najczęściej występuje w zastosowaniach praktycznych, gdzie wartości węzłowe pochodzą na przykład z pomiarów lub symulacji. Przybliżoną powierzchnię rysujemy łącząc węzły odcinkami.

Watkins w 1974 roku zaproponował algorytm maskowania pozwalający rysować kolejne krzywe (łamane) siatki rozpiętej na powierzchni będącej wykresem funkcji – rys.9.15. Można zauważyć, że dotychczas narysowany fragment (pierwszym takim fragmentem jest obszar powierzchni pomiędzy pierwszymi dwoma krzywymi/łamanymi) może zasłaniać wszystkie później rysowane elementy powierzchni. A zatem do realizacji algorytmu wystarczy zdefiniować bufor górny (ograniczenie górne Y_OG we współrzędnych rzutu) i bufor dolny (ograniczenie dolne Y_OD we współrzędnych rzutu), a następnie w każdym kroku sprawdzać położenie rysowanego fragmentu (odcinka) względem buforów. Jeśli element jest powyżej ograniczenia górnego lub poniżej dolnego to jest rysowany, w przeciwnym przypadku (między ograniczeniami) to nie jest rysowany (rys.9.15). Oczywiście każdy narysowany element powiększa (rozszerza w danym kierunku) odpowiednie ograniczenie.

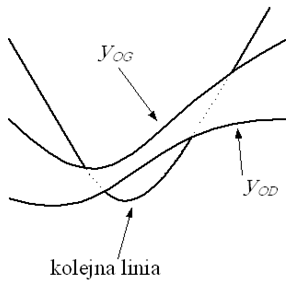
Rys.9.15. Idea algorytmu maskowania Watkinsa. Fragmenty rysowanej linii
między ograniczeniem dolnym (linia określona dla y_OD) a górnym (dla y_OG) są zasłonięte.

Standardowe podejście w algorytmie maskowania Watkinsa wymaga podczas rysowania analizy położenia odcinka względem łamanej (górnego ograniczenia lub dolnego). Tego typu zadanie jest klasycznym zadaniem geometrii obliczeniowej i nie należy do najprostszych – wymagałoby dodatkowego, znaczącego czasu realizacji. Można zmodyfikować problem tak, aby nie było to w ogóle konieczne.

W tym celu rozpatrzmy tę samą sytuację ale na mapie pikseli. Ograniczenia górne i dolne w tym przypadku odpowiadają zestawowi pikseli, które w kolejnych kolumnach określają minimalną i maksymalną wysokość. Rysując każdy nowy piksel wystarczy sprawdzić jego położenie względem tego minimum lub maksimum. A to jest operacją bardzo prosta. Jeśli nowy piksel jest powyżej maksimum (lub poniżej minimum) to jest rysowany, jeśli pomiędzy minimum i maksimum to rysowany nie jest. Oczywiście rysowany piksel przesuwa odpowiednie maksimum (lub minimum).

Zaproponowany mechanizm maskowania dla mapy pikseli może zostać połączony z algorytmem Bresenhama rysowania odcinka. Tak zmodyfikowany algorytm będzie rysował odcinki z uwzględnieniem rozstrzygania widoczności dla siatki rozpiętej na powierzchni będącej wykresem funkcji dwóch zmiennych – rys.9.16. Można pokazać że modyfikacja algorytmu Bresenhama wymaga dodania jednej instrukcji porównania i jednej instrukcji podstawienia. Nie zmienia to więc znacząco czasu realizacji samego rysowania odcinków.

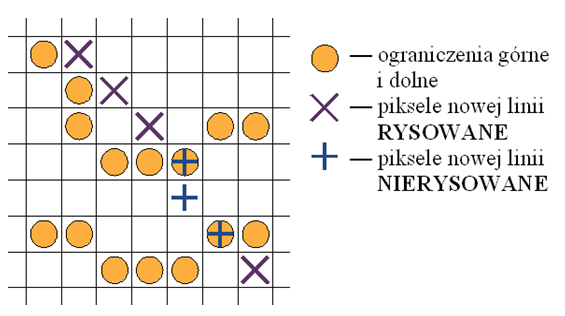
Rys.9.16. Podczas rysowania pikseli na mapie pikseli (np. algorytmem Bresenhama)
każdy piksel nowej linii jest sprawdzany. Jest rysowany tylko wtedy,
gdy znajduje się poza ograniczeniem dolnym i górnym.
Piksele pomiędzy ograniczeniami dolnym i górnym nie są rysowane.

Złożoność liniowa algorytmu wykorzystującego metodę maskowania Watkinsa wynosi O(n), gdzie n — liczba krawędzi wykresu (lub węzłów).

 Dodatkowo należy zwrócić  uwagę na kolejność wyboru do rysowania odcinków siatki. Jeśli byłyby one rysowane w naturalnej kolejności związanej z rodzinami linii dla stałego x, i dla stałego y, to mogłyby wystąpić problemy z wzajemnym zasłanianiem. Dobrym rozwiązaniem jest kolejność typu ZIG-ZAG (tzn. odcinki na przemian z każdej rodziny) lub kolejność zaproponowana na rysunku 9.17 a).

Warto dodatkowo zwrócić uwagę na fakt, że taka wersja algorytmu poprawnie pracuje tylko dla rzutu równoległego wykresu funkcji. Analiza rysowania na mapie pikseli z uwzględnieniem minimum i maksimum kolumny pokazuje, że dla odcinków rysowanych w rzucie perspektywicznym wystąpią błędy.

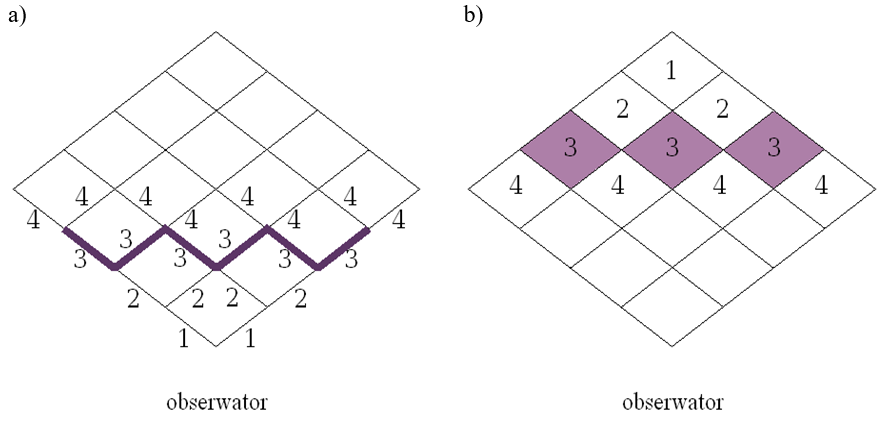
Rys.9.17. a) Kolejność ZIG-ZAG rysowania odcinków stosowana
w rysowaniu wykresu funkcji metodą maskowania Watkinsa.
b) Kolejność rysowania (wypełniania) czworokątów
przy zastosowaniu algorytmu malarskiego do rysowania wykresu funkcji.

Inną możliwością rysowania powierzchni wykresu funkcji jest zastosowanie algorytmu malarskiego. Oczywiście wykres funkcji pozwala zrezygnować z sortowania koniecznego w algorytmie malarskim. W tym przypadku wystarczy uwzględnić kolejność wynikającą z odległości „oczek” siatki dziedziny funkcji od obserwatora. Rysunek 9.17 b) pokazuje kolejność rysowania oczek siatki w takim przypadku. Oczka o tym samym numerze mogą być rysowane w dowolnej kolejności – nie zmienia to rysunku gdyż nie mogą się one wzajemnie zasłaniać.

Zastosowanie algorytmu malarskiego ma dodatkową zaletę: algorytm ten poprawnie rysuje powierzchnię będącą wykresem funkcji także dla rzutu perspektywicznego.

 Algorytm rysowania powierzchni będącej wykresem funkcji dwóch zmiennych jest przykładem algorytmu rozstrzygania widoczności dla szczególnej klasy obiektów trójwymiarowych. Drugim przykładem tego typu zadania jest algorytm rysowania figur obrotowych. Szczegóły tego algorytmu czytelnik może znaleźć w książce M.Jankowskiego Elementy grafiki komputerowej [3].