Podręcznik Grafika komputerowa i wizualizacja

W przypadku bryły dowolnej (a więc także wklęsłej) lub zestawu dowolnych brył, podział ścian na przednie i tylne nie wystarczy, gdyż taka analiza nie uwzględnia wzajemnego zasłaniania ścian (rys.9.5), jakie może wystąpić między obiektami lub ścianami tego samego obiektu. Problem taki występuje także dla zestawu brył wypukłych, tylko dla jednej bryły wypukłej można pokazać prostszy algorytm.

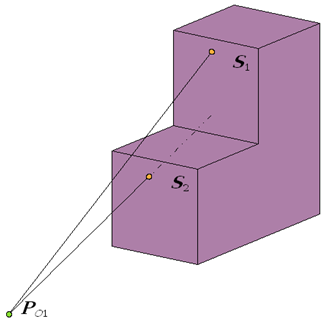
Rys.9.5. Co prawda obie ściany S1 i S2 są przednie, ale to nie jest warunkiem wystarczającym
aby były widoczne gdyż jedna ściana zasłania drugą.

 Naturalnym podejściem jest analiza wzajemnego położenia ścian, ale w takim przypadku trzeba przeanalizować wszystkie pary ścian (analiza „każdy z każdym”). Prowadzi to oczywiście do kwadratowej złożoności obliczeniowej algorytmu. Najprostszym mechanizmem przyspieszającym takie postępowanie jest test MINMAX czyli „opakowanie” wielokątów prostopadłościanami definiującymi minimum i maksimum po każdej współrzędnej dla danego wielokąta. Porównując wzajemne położenie prostopadłościanów opakowujących (co jest prostsze gdyż jest porównaniem minimów i maksimów współrzędnych) można wyeliminować wiele przypadków, gdy wielościany nie mogą się zasłaniać. Oczywiście takie postępowanie nie zmienia asymptotycznej złożoności obliczeniowej. Test MINMAX jest często stosowany do różnych algorytmów eliminacji elementów zasłoniętych.

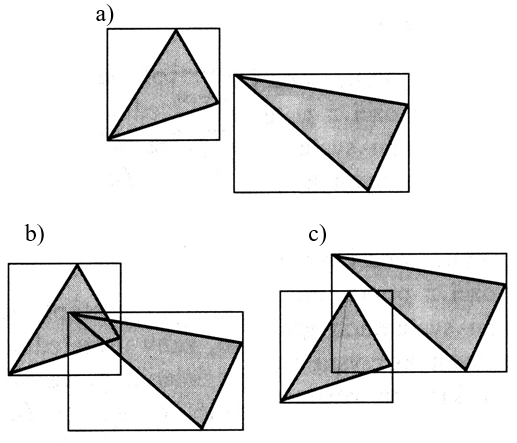
                  Rys.9.6. Test MINMAX – porównanie otoczenia: a) jeśli otoczenia prostokątne są rozłączne, 
to elementy nie mogą mieć punktów wspólnych i zasłaniać się,  
jeśli otoczenia nie są rozłączne, elementy mogą się zasłaniać (b) lub nie (c).

 Pierwszy algorytm rozstrzygania widoczności dla dowolnych brył, przy założeniu że ściany są trójkątami (a przecież dowolny wielokąt zawsze może zostać rozłożony na zbiór trójkątów) podał Ricci w 1972 roku. Był to algorytm pracujący metodą „każdy z każdym” o kwadratowej złożoności obliczeniowej.

Zasady spójności

Sutherland, Sproull i Schumacker zwrócili uwagę na pewną cechę analizy występującą w algorytmach określania widoczności. Jest nią spójność – pewne podobieństwo cech pozwalające wnioskować o zasłanianiu lub widoczności. Wyróżnia się:

 Jeśli na przykład rozpatrzymy scenę zawierającą wielościany, to o widoczności wierzchołków możemy np. wnioskować na podstawie widoczności ściany.: Jeśli ściana jest widoczna to również jej węzły są widoczne, Tego typu wnioski powinny być ostrożnie formułowane, gdyż nie wszystkie sytuacje są oczywiste (np. wniosek, że odcinek łączący widoczne węzły jest widoczny, nie zawsze jest prawdziwy.