Podręcznik Grafika komputerowa i wizualizacja
Rozdział 9. ELIMINACJA ELEMENTÓW ZASŁONIĘTYCH
9.2. Bryła wypukła i zorientowanie ściany, klasy algorytmów
Rozpatrzmy przypadek wielościanu wypukłego. Jest to jeden z przykładów problemu eliminacji elementów zasłoniętych, dla którego można pokazać kilka efektywnych i jednocześnie prostych algorytmów. Można zauważyć, że jeżeli na scenie jest dowolny wielościan wypukły (ale tylko jeden !), to wnioskowanie o widoczności jego elementów jest dość proste. Traktując taką scenę jako zbiór wielokątów (z których każdy jest oczywiście ścianą wielościanu), można ten zbiór podzielić na trzy grupy:
- Wielokąty widoczne przez obserwatora (wielokąty przednie).
- Wielokąty niewidoczne – zasłonięte (wielokąty tylne).
- Wielokąty, których rzut jest odcinkiem.
Wielokąty ostatniej grupy są pomijalne, odpowiednie odcinki zostaną i tak narysowane jeśli pojawią się wielokąty widoczne.
W pierwszej i drugiej grupie występują wielokąty, które w całości podlegają określonym zasadom widoczności i przynależności do grupy. Nie może zachodzić przypadek, że tylko część wielokąta jest widoczna (a druga część zasłonięta). A zatem rozwiązanie zadania wyboru elementów widocznych w przypadku wielościanu wypukłego sprowadza się do określenia zbioru wielokątów należących do pierwszej grupy. I one powinny być (w całości) narysowane.
Można pokazać kilka różnych sposobów rozwiązanie tak zdefiniowanego
zdania.
Rozwiązanie A
(pierwszy sposób) polega na analizie położenia obiektów w przestrzeni. Definiowane są określone
wektory a następnie jest wyznaczany iloczyn skalarny tych wektorów (rys.9.2).
Niech ![]() . Znak tego iloczynu
określa przynależność do określonej grupy: jeśli
. Znak tego iloczynu
określa przynależność do określonej grupy: jeśli ![]() to ściana S1 jest widoczna z punktu P0
. (ściana S1 jest przednia). Zwróćmy
uwagę na fakt, że w tym przypadku nie ma w ogóle mowy o jakimkolwiek rzucie.
Położenie obserwatora w przestrzeni w zupełności wystarczy.
to ściana S1 jest widoczna z punktu P0
. (ściana S1 jest przednia). Zwróćmy
uwagę na fakt, że w tym przypadku nie ma w ogóle mowy o jakimkolwiek rzucie.
Położenie obserwatora w przestrzeni w zupełności wystarczy.
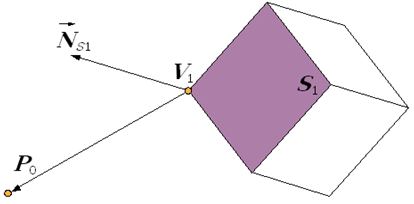
Rys.9.2. Wektory, na podstawie których badane jest zorientowanie ściany
(a w konsekwencji jej
zorientowanie).
Rozwiązanie B korzysta z informacji zarówno pochodzących z przestrzeni obiektu (sceny), jak i z informacji jakie dostarcza rzut. – Porównywane jest zorientowanie ściany obiektu (w przestrzeni obiektu) i zorientowanie rzutu ściany (w przestrzeni rzutu). Najpierw należy przypisać zorientowanie każdej ścianie, a następnie sprawdzić, czy zorientowanie rzutu ściany jest takie samo. Jeśli oba zorientowania są jednakowe, to ściana jest widoczna (przednia).
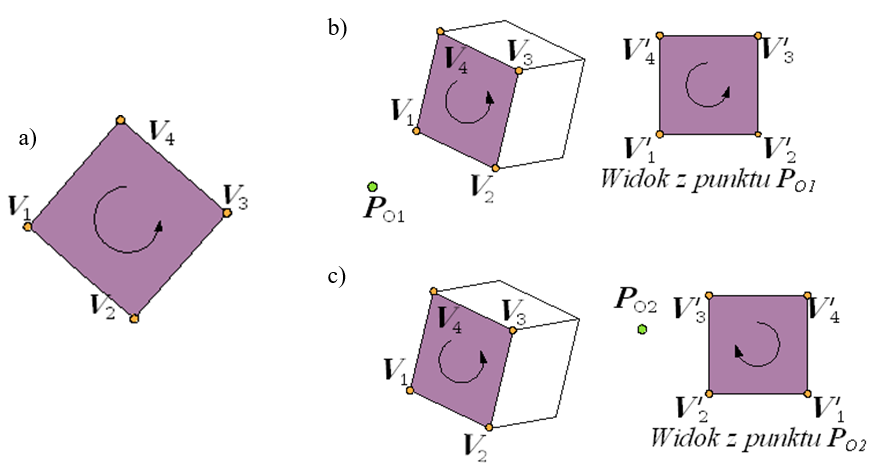
Rys.9.3. a)
Zorientowanie przypisane ścianie.
b) Porównanie
zorientowania ściany i zorientowania jej rzutu z punktu widzenia P01 .
c) Porównanie
zorientowania ściany i zorientowania jej rzutu z punktu widzenia P02 .
Zadanie określenia widoczności elementów wielościanu wypukłego można więc rozwiązać na dwa sposoby korzystając z rozwiązań A i B sprawdzających zorientowanie poszczególnych ścian.
Sposób A. Określić zorientowanie każdej ściany korzystając z rozwiązania A. Jeżeli ściana jest „przednia”, to jest widoczna.
Sposób B. Określić zgodność zorientowania każdej ściany korzystając z rozwiązania B. Jeśli orientacja ściany i jej rzutu są zgodne to ściana jest „przednia” i jest widoczna.
Analizę widoczności w przypadku wielościanu wypukłego, można przeprowadzić
opierając się tylko na informacji z przestrzeni rzutu – sposób C. W tym celu należy podzielić wierzchołki rzutu na dwa typy
– rysunek 9.4. Pierwszy typ (węzły: ![]() ) charakteryzuje się tym, że węzeł oraz zewnętrzne krawędzie
są widoczne. O pozostałych krawędziach i ich widoczności nie można nic
powiedzieć. Drugi typ (węzły:
) charakteryzuje się tym, że węzeł oraz zewnętrzne krawędzie
są widoczne. O pozostałych krawędziach i ich widoczności nie można nic
powiedzieć. Drugi typ (węzły:![]() ) charakteryzuje się tym , że co prawda nie można stwierdzić
czy węzeł jest widoczny czy nie, ale za to wszystkie elementy mają taki sam
atrybut. A więc jeśli jakaś jedna krawędź jest widoczna, to cały węzeł i
wszystkie jego krawędzie są widoczne.
) charakteryzuje się tym , że co prawda nie można stwierdzić
czy węzeł jest widoczny czy nie, ale za to wszystkie elementy mają taki sam
atrybut. A więc jeśli jakaś jedna krawędź jest widoczna, to cały węzeł i
wszystkie jego krawędzie są widoczne.
Korzystając z klasyfikacji węzłów można zaproponować sposób C wyznaczania widoczności elementów wielościanu wypukłego. Określając widoczność jednego węzła drugiego typu można przenieść ten sam atrybut widoczności do sąsiednich węzłów, przechodząc od jednego węzła do drugiego. W ten sposób powstają dwa komplementarne obrazy. W takim postępowaniu nie jest potrzebna informacja z przestrzeni obiektu. Wystarczy tylko informacja dotycząca rzutu.
Klasy algorytmów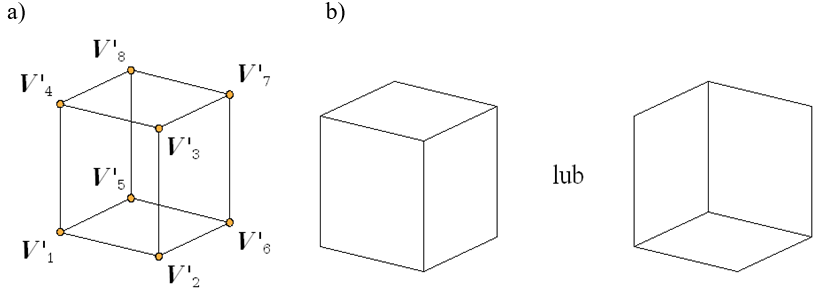
Rys.9.4. Na podstawie klasyfikacji węzłów (a) można
wyeliminować
węzły (i krawędzie) niewidoczne doprowadzając do rysunku b).
Najczęściej wyróżnia się trzy klasy algorytmów rozstrzygania widoczności
- Pracujące w przestrzeni obserwatora (np. sposób A).
- Pracujące w przestrzeni rzutu (np. sposób C).
- Wykorzystujące informacje z obu przestrzeni (np. sposób B).
Trzy sposoby rozwiązania problemu widoczności pokazują trzy sposoby wykorzystania informacji, pochodzących albo z przestrzeni obiektu (sceny), albo przestrzeni rzutu, albo obu. Oczywiście o ile w przypadku wielościanu wypukłego ten podział jest bardzo ostry i jednoznaczny, o tyle w przypadku dowolnego innego algorytmu podział będzie zdecydowanie mniej ostry i będzie oznaczał, że dany algorytm w większym stopniu wykorzystuje informację z jednej lub drugiej przestrzeni. Taki podział algorytmów można przeprowadzić dla dowolnych brył, nie tylko wypukłych.
Z drugiej strony często mówi się o precyzji obrazowej lub obiektowej danego algorytmu. Oznacza to, że algorytmy pracujące z precyzją obrazowa wykonują obliczenia z dokładnością urządzenia wyświetlającego (wynikającą z wyświetlania pojedynczego piksela). Algorytmy pracujące z precyzją obiektowa wykonują obliczenia z dokładnością związaną z definicją obiektów, a nie pikseli.
Aby określić złożoność algorytmów określania widoczności należy zdefiniować miarę złożoności sceny (obiektu). Najczęściej przyjmuje się, liczbę ścian jako taką miarę.
Złożoność trzech wariantów algorytmów eliminacji elementów zasłoniętych dla wielościanu wypukłego (sposoby A, B, C) jest liniowa. Jest to szczególny przypadek wśród algorytmów określania widoczności.
