Podręcznik
Wersja podręcznika: 1.0
Data publikacji: 01.01.2022 r.
Wykłady
W1…WN, odpowiadające w sumie ok. 10-12 godz. standardowego wykładu
2. Metoda płaszczyzn tnących
2.1. Wprowadzenie
Chcemy rozwiązać następujące zadanie programowania liniowego całkowitoliczbowego (ZPLC):
\( \max_{x\in X} x_0=c^Tx \)
\( X= \{ x: Ax \leq b, x \geq 0, \texttt{całkowitoliczbowe} \} \)
gdzie $A, b$ są całkowitoliczbowe.
Ograniczenia zadania modelują zależności wynikające bezpośrednio z treści zadania lub pośrednio, np. modelujące wymagane zależności logiczne lub inne powiązania między zmiennymi nie wyrażone bezpośrednio w zadaniu. Ja przykład może służyć wyznaczenie maksymalnej wartości z zmiennych, co zazwyczaj modeluje się dodatkową zmienną ograniczającą od góry zmienne stanowiące argument funkcji maksimum. Często problem można zamodelować w różny sposób, np. różnie ujmując ograniczenia, a nawet przyjmując różne definicje zmiennych decyzyjnych. Możemy więc mieć różne modele matematycznego dla danego problemu. Pytanie, które czy są modele "lepsze" lub "gorsze" z punktu widzenia zasobów potrzebnych do rozwiązania problemu.
\( \left[ \begin{array}{cc} 1 & 1 \\ -1 & 1 \\ 6 & 2 \\ \end{array} \right] \left[ \begin{array}{c} x_1 \\ x_2 \\ \end{array} \right] \leq \left[ \begin{array}{c} 5 \\ 0 \\ 21 \\ \end{array} \right] \)
\( x_1, x_2 \geq 0, \texttt{całkowitoliczbowe} \)
Zbiór rozwiązań dopuszczalnych jest następujący \( X=\{(0,0), (1,0), (2,0), (3,0), (1,1), (2,1), (3,1), (2,2)\} \) i na rysunku wygląda w następujący sposób:
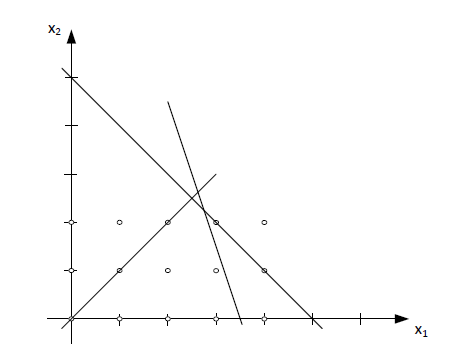
Ale zbiór \( X \) można opisywać na wiele sposobów, np.:
\( \left[ \begin{array}{cc} 1 & \frac{3}{2} \\ -1 & 1 \\ \frac{26}{5} & 4 \\ \end{array} \right] \left[ \begin{array}{c} x_1 \\ x_2 \\ \end{array} \right] \leq \left[ \begin{array}{c} 6 \\ 0 \\ 20 \\ \end{array} \right] \)
Wówczas zbiór rozwiązań dopuszczalnych wygląda jak na poniższym rysunku
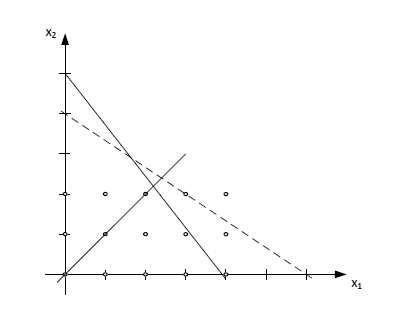
Który z opisów jest lepszy? Czy lepiej oznacza więcej czy mniej ograniczeń? Czy to ma znaczenie?
Najlepszy modele problemu jest opis zwarty, a więc taki, że wzystkie punkty zbioru dopuszczlnego \( X \) stają się wierzchołami wielościanu. Wówczas można pominąć warunek całkowitoliczbowości w modelu i rozwiązać problem liniowy ze zmiennymi ciągłymi, który jak wiemy jest znacznie prostszy obliczeniowo.
\( \left[ \begin{array}{cc} 1 & 1 \\ -1 & 1 \\ 6 & 0 \\ \end{array} \right] \left[ \begin{array}{c} x_1 \\ x_2 \\ \end{array} \right] \leq \left[ \begin{array}{c} 4 \\ 0 \\ 18 \\ \end{array} \right] \)
\(x_1, x_2 \geq 0, \texttt{całkowitoliczbowe}\)
Ten najbardziej zwarty opis na rysunku wygląda następująco:
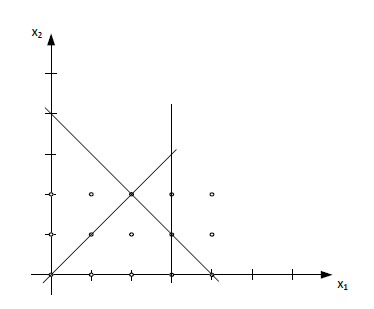
\(conv(X)=\{x: x=\sum_{i\in T} \lambda_ix^i, \sum_{i \in T} \lambda_i=1, \lambda_i \geq 0\texttt{ dla }i \in T\} \)
jest nazywany uwypukleniem zbioru \(X\) (otoczką wypukłą zbioru \(X\)).
Dla każdego zbioru \(X=P \cap \mathbb{Z}^n\), przy czym \(P=\{x\in \mathbb{R}^n_+, Ax \leq b\}\) jest opisem wielościennym tego zbioru, zachodzi \(X \subseteq conv(X) \subseteq P\).
Dla każdego zbioru \(X=P \cap \mathbb{Z}^n\), przy czym \(P=\{x\in \mathbb{R}^n_+, Ax \leq b\}\) jest opisem wielościennym tego zbioru, zachodzi \(X \subseteq conv(X) \subseteq P\).
Sformułowanie 1
\( \sum_{j=1}^n x_{ij} = 1 \qquad i=1, \ldots, m \\ \sum_{i=1}^m x_{ij} \leq mv_j \qquad j=1, \ldots, n \\ x_{ij} \geq 0, v_j \in\{0,1\} \qquad \forall i,j \)
Sformułowanie 2
\( \sum_{j=1}^n x_{ij} = 1 \qquad i=1, \ldots, m \\ x_{ij} \leq v_j \qquad \forall i,j \\ x_{ij} \geq 0, v_j \in\{0,1\} \qquad \forall i,j \)
Rozważym przykład dla dwóch lokalizacji i dwóch klientów.
Sformułowanie 1
\( x_{1,1} + x_{1,2} = 1 \\ x_{2,1} + x_{2,2} = 1 \\ x_{1,1} + x_{2,1} \leq 2v_1 \\ x_{1,2} + x_{2,2} \leq 2v_2 \)
Zobaczmy przestrzeń rozwiązań dopuszczalnych np. dla \(x_{1,1}=1\), \(x_{2,1}=0\) to \(v_1 \in \langle 0,5;1 \rangle\):
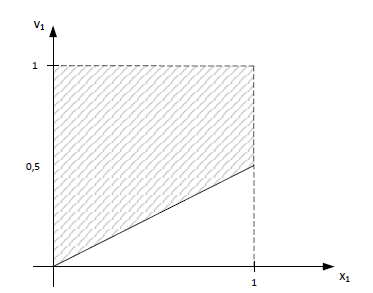
Sformułowanie 2
\( x_{1,1} + x_{1,2} = 1 \\ x_{2,1} + x_{2,2} = 1 \\ x_{1,1} \leq v_1 \\ x_{2,1} \leq v_1 \\ x_{1,2} \leq v_2 \\ x_{2,2} \leq v_2 \)
Teraz dla \(x_{1,1}=1\) to \(v_1=1\) wygląda w następujący sposób:
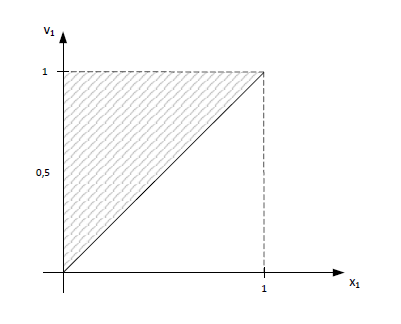
Rysunki wskazują, że sformułowanie 2 jest silniejsze (przynajmniej w rozważanym obszarze).
