Podręcznik
Wersja podręcznika: 1.0
Data publikacji: 01.01.2022 r.
Wykłady
W1…WN, odpowiadające w sumie ok. 10-12 godz. standardowego wykładu
1. Metoda generacji kolumn
Wprowadzenie
Wiele zagadnień związanych z badaniami operacyjnymi jest formułowanych w sposób ścisły lub przybliżony przy pomocy modeli programowania liniowego. Opracowanie algorytmu sympleks pozwoliło na stosunkowo łatwe wyznaczanie rozwiązań optymalnych takich zadań. Pomimo, że w najgorszym przypadku złożoność obliczeniowa tego algorytmu rośnie wykładniczo, to jednak przeciętnie zadania są rozwiązywane bardzo efektywnie.
Istnieje jednak grupa problemów, które choć formalnie zaliczają się do zadań programowania liniowego, to jednak rozwiązanie ich klasycznymi metodami jest nieopłacalne, głównie ze względu na wielkość zajmowanej pamięci, ale także ze względu na czas obliczeń. Cechą charakterystyczną tych zadań jest występowanie bardzo dużej liczby zmiennych, przy stosunkowo niewielkiej liczbie ograniczeń. W niektórych przypadkach liczba zmiennych może być nieskończona lub trudna do wyznaczenia. Oczywiste jest, że przechowywanie w pamięci całej macierzy ograniczeń takiego zadania oraz wykonywanie przekształceń na wszystkich jej elementach jest niemożliwe, a w najlepszym razie nieefektywne.
Rozwiązaniem jest zastosowanie metody generacji kolumn. Jest ona oparta na skorygowanej metodzie sympleks, w której przechowuje się tylko aktualną macierz bazową. Różnica między obydwiema metodami polega na tym, że w metodzie generacji kolumn nowe kolumny wprowadzane do bazy w każdej iteracji nie są bezpośrednio wyszukiwane w macierzy ograniczeń, lecz są wyznaczane w oddzielnym zadaniu optymalizacji.
Skorygowana metoda prymalna sympleks
Rozważmy następujące zadanie programowania liniowego:
Zmaksymalizować
![]()
Przy ograniczeniach
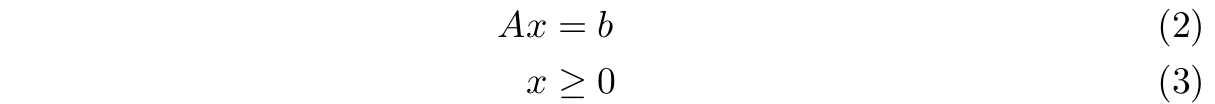
Załóżmy, że kolumny macierzy \( A \) zostały przedstawione w taki sposób, że \(A = (B, N )\), gdzie \(B\) jest macierzą bazową o wymiarach \(m\) × \(m\) (det \(B \ne 0\)), \(N\) jest macierzą utworzoną z pozostałych kolumn macierzy \(A\). Niech ponadto \(x = (x_B , x_N )\), gdzie \(x_B\) jest wektorem zmiennych bazowych odpowiadających kolumnom macierzy \(B\), natomiast \(x_N\) jest wektorem zmiennych niebazowych odpowiadających kolumnom macierzy \(N\) . Warunek \(Ax = b\) możemy teraz zapisać następująco:
![]()
Ponieważ \(B\) jest macierzą nieosobliwą, zatem istnieje macierz odwrotna \(B^{−1}\) . Możemy więc wyrazić \(x_B\) w zależności od \(x_N\) :
![]()
Rozwiązanie bazowe \(x_B = B^{-1} b\) otrzymujemy, gdy zmienne niebazowe \(x_N\) są na swoich dolnych ograniczeniach, czyli \(x_N = 0\). Twierdzenie mówiące, że jeśli zadanie programowania liniowego ma rozwiązanie optymalne, to ma również rozwiązanie bazowe optymalne, pozwala nam, przy poszukiwaniu rozwiązania optymalnego, ograniczyć się tylko do przeszukiwania rozwiązań bazowych dopuszczalnych.
W algorytmie skorygowanej metody prymalnej sympleks, wychodząc od dowolnego dopuszczalnego rozwiązania bazowego, znajdujemy kolejno inne dopuszczalne rozwiązania bazowe polepszające wartość fukcji celu \(x_0\) . Przejście pomiędzy dwoma kolejnymi dopuszczalnymi rozwiązaniami bazowymi odbywa się poprzez wprowadzenie do bazy jednej ze zmiennych niebazowych.
Załóżmy, że mamy wyjściowe rozwiązanie bazowe określone wzorem (5). Chcemy teraz znaleźć inne dopuszczalne rozwiązanie bazowe dające większą wartość funkcji celu \(x_0\) . Niech \(c = (cB , cN )\), wtedy
![]()
wykorzystując równanie (5) eliminujemy \(x_B\) i otrzymujemy
![]()
Po podstawieniu \(x_N = 0\) w powyższym równaniu otrzymujemy wartość rozwiązania bazowego równą \(x_0 = c_B B^{−1} b\). Zapiszmy równania (5) i (7) w następujący sposób
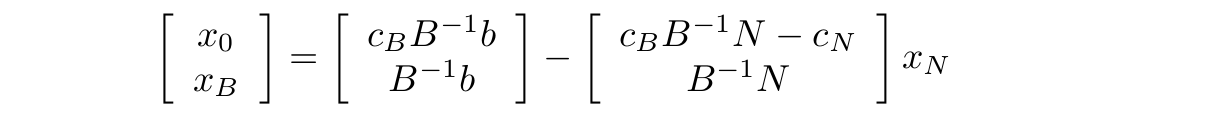
Oznaczmy przez \(x_B_0\) wartość funkcji celu \(x_0\) , a przez \( x_{B_{1}}, ..., x_{B_{m}} \) elementy wektora xB . Niech N będzie zbiorem indeksów kolumn macierzy N , a ponadto
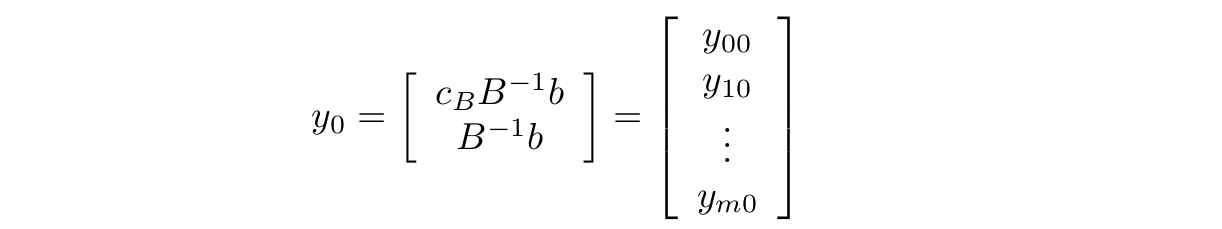
oraz

gdzie \(a_j , j \in N\) , jest kolumną macierzy \(N\) . Możemy teraz równania (5) i (7) zapisać następująco:
![]()
Zadaniem naszym jest wybór takiej zmiennej niebazowej, aby, po wprowadzeniu jej do bazy, nowe rozwiązanie było lepsze od poprzedniego. Załóżmy, że do bazy chcemy wprowadzić jedną ze zmiennych niebazowych \(x_k (k \in N )\). Spróbujmy więc stopniowo zwiększać wartość zmiennej \(x_k\) , która do tej pory była na swym dolnym ograniczeniu. Z równania (8) widzimy, że wartość funkcji celu \(x_{B_{0}}\) będzie się zwiększała tylko wtedy, gdy \(y_{0k}\) będzie mniejsze od zera. Oznacza to, że zmienną wprowadzaną do bazy możemy wybrać tylko spośród tych zmiennych niebazowych \(x_j\) , dla których parametry \(y_{0j}\) nazywane cenami zredukowanymi są ujemne (\(y_{0j} = c_B B^{−1} a_j − c_j < 0)\). Zauważmy, że zwiększaniu się zmiennej \(x_k\) towarzyszy także zmiana wartości zmiennych bazowych \(x_{B_{i}} (i = 1, . . . , m)\). Ponieważ wartość żadnej z nich nie może być ujemna, to, jeśli któryś ze współczynników \(y_{ik}\) w równaniach (8) jest dodatni, wtedy określa on maksymalną wartość, którą może przyjąć zmienna \(x_k\) bez naruszenia ograniczenia \(x_{B_{i}} > 0\):
![]()
Ponieważ ograniczenie to musi być spełnione dla wszystkich zmiennych bazowych \(x_{B_{i}}\) , to
![]()
Po osiągnięciu przez wybraną zmienną niebazową \(x_k\) wartości \(x_k\) max jedna lub kilka zmiennych bazowych znajdzie się na swym dolnym ograniczeniu; spośród nich wybieramy zmienną, która zostanie usunięta z bazy.
Zmienną niebazową wprowadzaną do bazy może być dowolna zmienna \(x_k (k \in N )\), dla której \(y_{0k} < 0\). Na ogół jednak, w celu polepszenia szybkości zbieżności, wybiera się taką zmienną \(x_k\) dla której
![]()
Algorytm skorygowanej metody prymalnej sympleks
W algorytmie skorygowanej metody prymalnej sympleks nie operuje się tzw. macierzą sympleksową, lecz macierzą bazową oraz całą macierzą ograniczeń. W każdej iteracji przegląda się wszystkie kolumny aj odpowiadające zmiennym niebazowym. Poszczególne kroki algorytmu przedstawiają się następująco:

Należy pamiętać o tym, że, tak jak w zwykłej metodzie sympleksowej, wyłącznie zmienne bazowe mogą przyjmować wartości niezerowe i, wraz z odpowiadającymi im kolumnami, stanowią pełne rozwiązanie zadania (1)–(3).
Wykrywanie nieograniczoności
k-tej nie jest większy od zera, wtedy możliwy jest nieograniczony wzrost zmiennej niebazowej \(x_k\) bez naruszenia ograniczenia na zmienne bazowe \(x_{B_{i}} > 0\), a to pociąga za sobą nieograniczony wzrost wartości funkcji celu \(x_0 = y_{i0} − y_{0k} x_k\) .
Sytuacja taka oznacza, że rozwiązywane przez nas zadanie jest nieograniczone i algorytm powinien zostać w tym momencie przerwany.
Wyznaczanie początkowego dopuszczalnego rozwiązania bazowego
Rozpoczęcie obliczeń metodą sympleksową jest uwarunkowane znajomością początkowego dopuszczalnego rozwiązania bazowego. Jeśli początkowe dopuszczalne rozwiązanie bazowe nie jest łatwo dostępne, wtedy trzeba je wygenerować rozwiązując skorygowaną prymalną metodą sympleksową następujące zadanie pomocnicze:
Zmaksymalizować
![]()
przy ograniczeniach
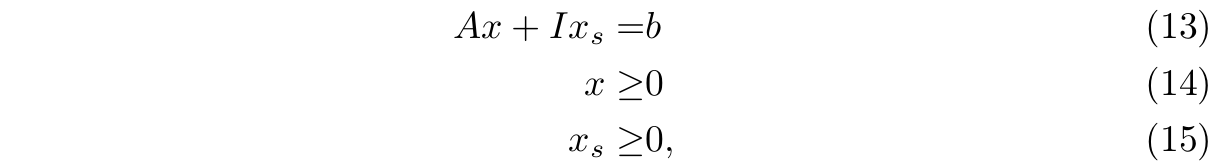
gdzie \(b \ge 0\), a \(x_s\) jest m-wymiarowym wektorem tzw. zmiennych sztucznych.
Dla zadania tego można z łatwością określić początkowe dopuszczalne rozwiązanie bazowe \({x \brack x_s} = { 0 \brack b }\). Po zakończeniu rozwiązywania tego zadania mogą wystąpić następujące przypadki:
- 1) min ŵ = w < 0 – zbiór rozwiązań dopuszczalnych zadania wyjściowego jest pusty (zadanie wyjściowe jest sprzeczne).
- 2) ŵ = 0 i wśród zmiennych bazowych nie występują zmienne sztuczne – wyznaczono początkowe dopuszczalne rozwiązanie bazowe.
- 3) ŵ = 0 i wśród zmiennych bazowych występują zmienne sztuczne. Możliwe są wówczas dwa warianty:
- a) Zmienna bazowa \(x_{B_{i}}\) jest zmienną sztuczną oraz \(y_{ij} = 0\) dla każdego \(j \in N\) – w zadaniu wyjściowym występuje redundancja.
- b) Zmienna bazowa \(x_{B_{i}}\) jest zmienną sztuczną oraz istnieje \(j \in N\) takie, że \(y_{ij} \ne 0\) – należy zastąpić zmienną \(x_{B_{i}}\) zmienną \(x_j\) , a otrzymane początkowe dopuszczalne rozwiązanie bazowe jest zdegenerowane (istnieją zmienne bazowe równe 0).
Metoda generacji kolumn
W skorygowanej metodzie prymalnej sympleks posługujemy się w sposób jawny całą macierzą ograniczeń – z góry znamy liczbę kolumn oraz jej zawartość. Możemy jednak łatwo dojść do wniosku, że znajomość całej macierzy ograniczeń nie jest konieczna. W każdym kroku wstawiamy do macierzy bazowej nową kolumnę odpowiadającą zmiennej niebazowej, nie jest jednak istotne czy nowa kolumna została wybrana z podanej ‘explicite’ macierzy ograniczeń, czy też została wyliczona w jakiś inny sposób. Najważniejsze jest aby odpowiadająca tej kolumnie cena zredukowana \(y_{0j}\) była jak najmniejsza, a jeśli jest przy tym ujemna, to wprowadzenie nowej kolumny spowoduje poprawienie poprzedniego rozwiązania. Zadanie wyznaczenia nowej kolumny możemy więc w sposób ogólny zapisać następująco:
![]()
gdzie \(a_j\) jest szukanym wektorem zmiennych minimalizującym cenę zredukowaną \(y_{0j}\) , który jako nowa kolumna zostanie wprowadzony do macierzy bazowej (indeks \(j\) ma tylko znaczenie symboliczne), \(\pi = c_B B^{ −1}\) – wektor cen dualnych, \(c_j\) – cena w funkcji celu odpowiadająca znalezionej kolumnie.
Zauważmy, że jeśli w wyniku rozwiązania tego zadania otrzymamy kolumnę, która już znajduje się w bazie, to wartość ceny zredukowanej odpowiadającej tej kolumnie będzie wynosiła 0, czyli nastąpi zakończenie algorytmu.
Metoda generacji kolumn działa analogicznie do skorygowanej metody prymalnej sympleks z tą tylko różnicą, że nowe kolumny wstawiane w każdym kroku do macierzy bazowej są wyznaczane w oddzielnym zadaniu optymalizacji. Takie podejście pozwala na rozwiązywanie zadań z macierzą ograniczeń o potencjalnie nieskończonej liczbie kolumn. Nie jest bowiem konieczne pamiętanie całej tej macierzy; do znalezienia kolejnego dopuszczalnego rozwiązania bazowego wystarczy znajomość aktualnej macierzy bazowej.
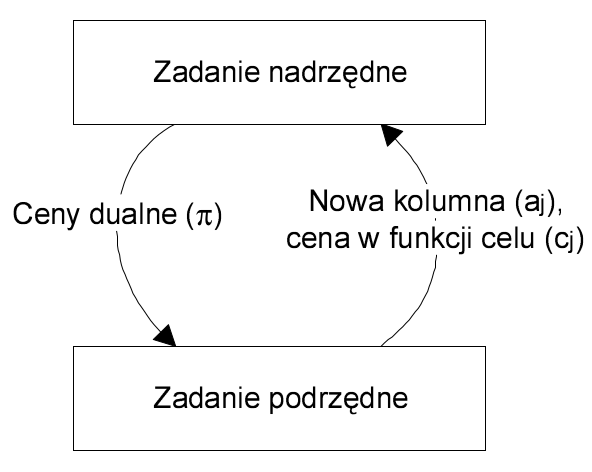
Na poniższym rysunku przedstawiono schemat działania metody generacji kolumn. Możemy wyróżnić zadanie nadrzędne, będące głównym zadaniem optymalizacji oraz zadanie podrzędne. W każdej iteracji do zadania podrzędnego przekazywany jest wektor cen dualnych \(\pi\), który służy do obliczenia nowej kolumny \(a_j\). Kolumna ta jest następnie zwracana do zadania nadrzędnego.
Zadanie podrzędne
W zadaniu podrzędnym wyznaczane są kolumny z macierzy ograniczeń o najmniejszych wartościach ceny zredukowanej \(y_{0j}\) . Aby zadanie to miało sens, na kolumnę \(a_j\) muszą zostać nałożone pewne ograniczenia. Na przykład można ograniczyć zakres wartości jakie mogą przyjmować poszczególne elementy kolumny \(a_j\) : \(d \le [a_j ]_{i=1,...,m} \le e\). Ograniczenia nałożone na rozwiązanie zadania podrzędnego zawężają zbiór kolumn, które mogą być wstawione do macierzy bazowej zadania nadrzędnego, czyli – zbiór wszystkich rozwiązań dopuszczalnych zadania podrzędnego określa wszystkie możliwe kolumny występujące w macierzy ograniczeń zadania nadrzędnego. Jeżeli na przykład do ograniczenia \(d \le [a_j]_{i} \le e\) dodamy warunek całkowitoliczbowości, wtedy macierz ograniczeń zadania nadrzędnego będzie składała się ze skończonej liczby kolumn, w których każdy element musi należeć do przedziału [d, e] i być liczbą całkowitą. Bardziej złożone ograniczenia nakładane na kolumny wyznaczane w zadaniu podrzędnym zostały przedstawione w przykładach w dalszej części tej pracy.
W metodzie generacji kolumn, poza wyznaczeniem w kolejnej iteracji nowej kolumny wstawianej do macierzy bazowej, konieczne jest określenie wartości ceny cj w funkcji celu odpowiadającej tej kolumnie. Cena ta na ogół nie jest podana w sposób jawny, lecz zależy od wyznaczanego wektora \(a_j\) : \(c_j = f (a_j )\). Skutkiem tego może być poważne zwiększenie złożoności funkcji celu zadania podrzędnego
![]()
