Podręcznik
Wymagania zaliczenia
Wersja podręcznika: 1.0
Data publikacji: 01.01.2022 r.
Wykłady
W1…WN, odpowiadające w sumie ok. 10-12 godz. standardowego wykładu
1. Modelowanie celów i preferencji
1.1. Optymalizacja wielokryterialna
Zadanie optymalizacji wielokryterialnej (wielokryterialne zadanie programowania matematycznego) może być sformułowane następująco:
Nawet nie znając relacji preferencji (wiedząc jedynie, że jest to racjonalna relacja preferencji), możemy stwierdzić, że pewne wektory ocen nie mogą być maksymalne w sensie danej relacji. Wynika to z faktu, że pewne wektory ocen są gorsze od innych dla wszystkich racjonalnych relacji preferencji. Można to sformalizować za pomocą relacji racjonalnej dominacji. Ponieważ model racjonalnych relacji preferencji jest najogólniejszym modelem preferencji, relacje racjonalnej dominacji nazywa się po prostu relacją dominacji.
\(\max\{(f_1({\bf x}), f_2({\bf x}), \ldots, f_m({\bf x})) : {\bf x} \in Q\}\),
gdzie
- \({\bf f} = (f_1, f_2, \ldots, f_m)\) jest funkcją (wektorową) przekształcającą przestrzeń decyzji \(X = R^n\) w przestrzeń ocen \(Y = R^m\);
- poszczególne współrzędne \(f_i\) reprezentują skalarne funkcje oceny;
- \(I = \{1, 2, \ldots, m\}\) jest zbiorem indeksów ocen;
- \(Q \subset X\) oznacza zbiór dopuszczalny (zbiór decyzji dopuszczalnych);
- \({\bf x} \in X\) oznacza wektor zmiennych decyzyjnych.
Zakładamy, że wybór decyzji (rozwiązania) bierze pod uwagę tylko wektory ocen i decyzje o jednakowych wektorach ocen są jednakowo dobre. Tym samym problem wyznaczenia najlepszej decyzji możemy ograniczyć do zagadnienia wyboru najlepszego wektora ocen w zbiorze ocen osiągalnych (osiągalnych wektorów ocen)
\(A = \{{\bf y} : {\bf y} = {\bf f}({\bf x}), {\bf x} \in Q\}\)
podczas gdy odpowiednia decyzja prowadząca do wybranego wektora ocen może być zidentyfikowana w końcowej fazie analizy problemu. Prowadzi to do modelu wielokryterialnego w przestrzeni ocen
\(\max\{ {\bf y} = (y_1, \ldots, y_m) : {\bf y} \in A\}\),
gdzie oceny są bezpośrednio określone jako pojedyncze zmienne.
Rozpatrzmy dwukryterialne zadanie programowania liniowego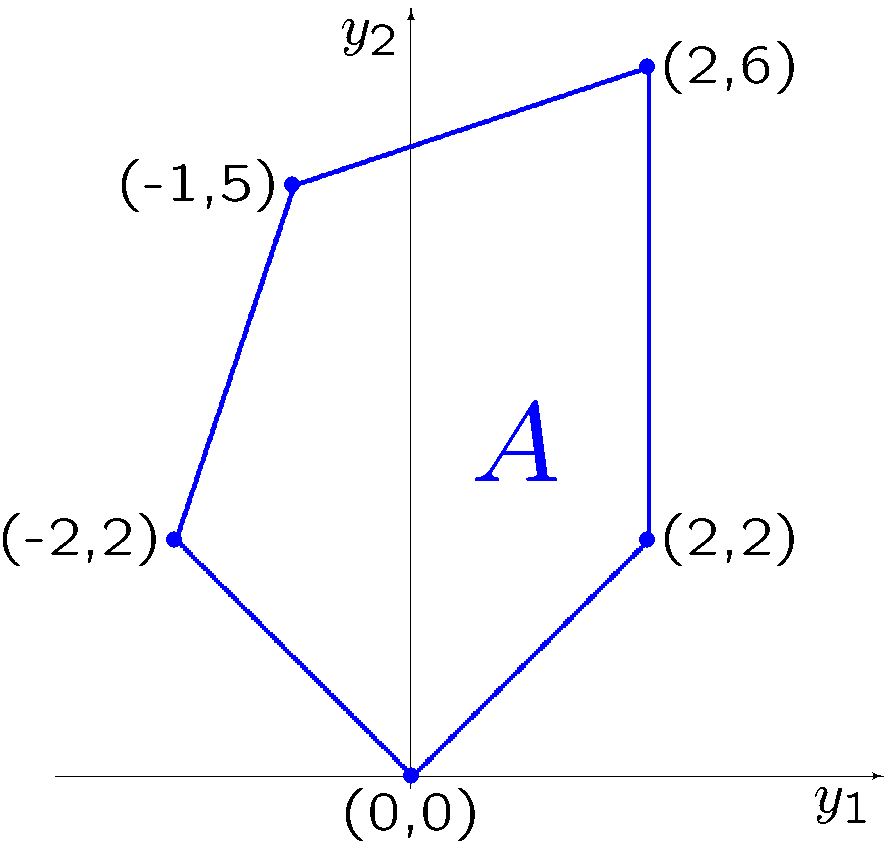
W odróżnieniu od modeli optymalizacji jednokryterialnej model decyzyjny optymalizacji wielokryterialnej nie precyzuje ściśle jednej koncepcji najlepszego (optymalnego) rozwiązania. Zapis maksymalizacji w modelu wielokryterialnym oznacza jedynie, że dla każdej pojedynczej oceny preferowana jest większa wartość.
Tym samym, rozważane preferencje są reprezentowane przez racjonalne relacje preferencji, spełniające warunki zwrotności, przechodniości i ścisłej monotoniczności.\(\begin{array}{rl}
\max & (x_2 - x_1, x_1 + x_2)\\
\mbox{p.w.} & -x_1 + x_2 \le 2\\
\max & (x_2 - x_1, x_1 + x_2)\\
\mbox{p.w.} & -x_1 + x_2 \le 2\\
& 2x_1 + x_2 \le 8\\
& 2x_1 - x_2 \ge 4\\
& x_1, x_2 \ge 0.\\
\end{array}\)
\end{array}\)
W przestrzeni decyzji zbiór dopuszczalny jest pięciokątem o
wierzchołkach (0,0), (0,2), (2,4), (3,2) i (2,0). Kierunki maksymalizacji dla pojedynczych ocen są określone odpowiednimi warstwicami (por. poniższy rysunek).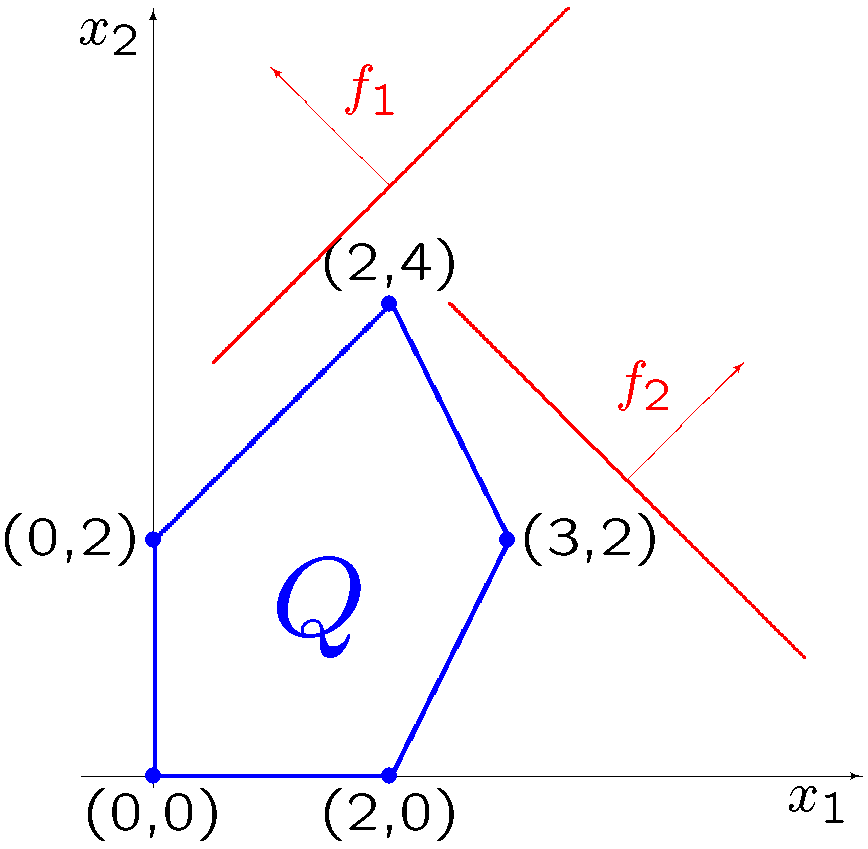

Dwukryterialne zadanie programowania liniowego w przestrzeni decyzji
Ponieważ funkcje wyrażające oceny są liniowe, a zbiór dopuszczalny jest uwypukleniem swoich pięciu wierzchołków, to obraz zbioru dopuszczalnego w przestrzeni ocen jest uwypukleniem obrazu wierzchołków. Tym samym, zbiór ocen osiągalnych \(A\) przyjmuje postać pięciokąta
przedstawionego na poniższym rysunku, gdzie wierzchołek (0,0) jest obrazem punktu (0,0), wierzchołek (-2,2) jest obrazem punktu (0,2), wierzchołek (2,6) jest obrazem punktu (2,4), wierzchołek (-1,5) jest obrazem punktu (3,2), wierzchołek (2,2) jest obrazem punktu (2,0).
Dwukryterialne zadanie programowania liniowego w przestrzeni ocen
Kierunki maksymalizacji poszczególnych ocen pokrywają się z osiami układu współrzędnych.Nawet nie znając relacji preferencji (wiedząc jedynie, że jest to racjonalna relacja preferencji), możemy stwierdzić, że pewne wektory ocen nie mogą być maksymalne w sensie danej relacji. Wynika to z faktu, że pewne wektory ocen są gorsze od innych dla wszystkich racjonalnych relacji preferencji. Można to sformalizować za pomocą relacji racjonalnej dominacji. Ponieważ model racjonalnych relacji preferencji jest najogólniejszym modelem preferencji, relacje racjonalnej dominacji nazywa się po prostu relacją dominacji.
Relacja dominacji. Mówimy, że wektor ocen \(\bf y^\prime\) (racjonalnie) dominuje \(\bf y^{\prime\prime}\), lub \(\bf y^{\prime\prime}\) jest (racjonalnie) dominowany przez \(\bf y^\prime\) wtedy i tylko wtedy, gdy \(\bf y^\prime \succ \bf y^{\prime\prime}\) dla wszystkich racjonalnych relacji preferencji.
Relacja dominacji zazwyczaj nie spełnia warunku spójności i dlatego może istnieć wiele wektorów ocen maksymalnych w sensie relacji racjonalnej dominacji, z których żaden nie jest największy. To znaczy, na ogół nie istnieje wektor ocen dominujący wszystkie pozostałe. Zatem relacja dominacji nie pozwala na jednoznaczne określenie najlepszego wektora ocen. Umożliwia ona jedynie wyróżnienie zbioru niezdominowanych wektorów ocen w odróżnieniu od zdominowanych wektorów ocen. Zdominowane wektory ocen odpowiadają oczywiście decyzjom nieoptymalnym, ponieważ są one gorsze od innych osiągalnych wektorów ocen w sensie każdej racjonalnej relacji preferencji. Jeżeli wektor ocen \(\bf y^{\prime\prime}\) jest dominowany przez \(\bf y^\prime\), to może on być wyeliminowany z
poszukiwań, ponieważ wszyscy racjonalni decydenci preferują \(\bf y^\prime\) w stosunku do \(\bf y^{\prime\prime}\). Wystarczy zatem ograniczyć poszukiwania właściwego wyboru do niezdominowanych wektorów ocen.
Osiągalny wektor ocen \({\bf y} \in A\) nazywamy (racjonalnie) niezdominowanym
wtedy i tylko wtedy, gdy nie istnieje \({\bf y^\prime} \in A\) taki, że \(\bf y\) jest dominowany przez \(\bf y^\prime\).
Pojęcie niezdominowanych wektorów ocen dotyczy elementów przestrzeni ocen \(Y\). W wielokryterialnym problemie decyzyjnym interesują nas raczej odpowiednie wektory dopuszczalne w przestrzeni decyzji \(X\).
Rozwiązania efektywne. Wektor dopuszczalny \({\bf x} \in Q\) nazywamy rozwiązaniem efektywnym (Pareto-optymalnym, sprawnym) zadania optymalizacji wielokryterialnej wtedy i tylko wtedy, gdy odpowiadający mu wektor ocen \({\bf y} = {\bf f}({\bf x})\) jest wektorem niezdominowanym.
Pojedyncze rozwiązania efektywne zadania optymalizacji wielokryterialnej można wyznaczać poszukując w zbiorze ocen osiągalnych \(A\) wektorów największych w sensie pewnej spójnej racjonalnej relacji preferencji. W szczególności, można w tym celu rozwiązywać jednokryterialne skalaryzacje zadania.