Podręcznik

1. Modelowanie celów i preferencji

1.4. Metody punktu odniesienia

Zauważmy, że model zadowalający pomija możliwość osiągnięcia poziomów aspiracji przez wszystkie oceny. Faktycznie, w typowym procesie decyzyjnym realizowanym przez decydenta poziomy aspiracji są na ogół stawiane w postaci wielkości nieosiągalnych, a przynajmniej nieosiągalnych jednocześnie. Tym samym, osiągnięcie wszystkich poziomów aspiracji jest sytuacją nierealną. Inaczej rzecz się ma w przypadku systemu wspomagania decyzji i optymalizacji parametrycznej skalaryzacji. Tutaj, model decyzyjny może być wykorzystywany początkowo do rozpoznawania problemu i poziomy aspiracji mogą być wielokrotnie określane próbnie w postaci różnych wielkości. Mogą to być wartości osiągalne, a jednocześnie optymalizacja skalaryzacji umożliwia łatwe wynaczanie rozwiązań najlepszych. Dlatego istotne jest uściślenie modelu decyzyjnego o przypadek osiągalnych poziomów aspiracji. Prowadzi to do tzw. quasi-zadowalającego modelu procesu decyzyjnego wprowadzonego przez Wierzbickiego.

W quasi-zadowalającym (quasi-satysfakcyjnym) modelu procesu decyzyjnego przyjmuje się, że decydent rozwiązując problem decyzyjny określa poziomy aspiracji jako pożądane wartości poszczególnych ocen. Jeżeli wartości ocen nie osiągają poziomów aspiracji, to decydent stara się znaleźć lepsze rozwiązanie. Jeżeli wartości pewnych ocen osiągnęły odpowiednie poziomy aspiracji, to decydent koncentruje uwagę na poprawie wartości tych ocen, które nie osiągnęły swoich poziomów aspiracji. Jeżeli wszystkie oceny osiągną założone poziomy aspiracji, to decydent jest zainteresowany dalszą poprawą ocen, o ile jest to możliwe.

Istnieje możliwość konstrukcji parametrycznych skalaryzacji wykorzystujących poziomy aspiracji jako główne parametry sterujące w procesie analizy interaktywnej, a jednocześnie spełniających zasadę niezdominowania rozwiązań. Techniki parametrycznej skalaryzacji spełniające postulaty:

• zasadę niezdominowania rozwiązań,
• zupełnej parametryzacji zbioru niezdominowanego,
• efektywności obliczeniowej,
• intuicyjności i sterowalności parametrów sterujących

umożliwiają implementację systemu wspomagania decyzji, pozwalającego interaktywnie wyznaczyć satysfakcjonujące rozwiązanie efektywne zgodne z preferencjami decydenta. Taką techniką (a właściwie rodziną technik) jest metoda punktu odniesienia (ang. reference point method).

Metody punktu odniesienia (MPO) łączą prostotę i otwartość sterowania procesem analizy interaktywnej ze ścisłym przestrzeganiem zasady niezdominowania generowanych rozwiązań i zupełnej parametryzacji zbioru niezdominowanego. Używają one poziomów aspiracji jako głównych parametrów sterujących, ale interpretują je zgodnie z zasadami modelu quasi-zadowalającego. Dokładniej, model preferencji reprezentowany przez skalaryzacje używane w metodach punktu odniesienia spełnia następujące dwa postulaty:

P1. Relacja preferencji jest racjonalną relacją preferencji, czyli przestrzegana jest zasada niezdominowania.
P2. Rozwiązanie ze wszystkimi indywidualnymi ocenami $y_i$ równymi odpowiadającym im poziomom aspiracji jest preferowane w stosunku do rozwiązania z przynajmniej jedną indywidualną oceną gorszą (mniejszą) od odpowiedniego poziomu aspiracji.

Klasyczna metoda punktu odniesienia polega na maksymalizacji funkcji skalaryzującej

$s({\bf y}) = \min_{i=1,\ldots,m} s_i(a_i,y_i) + \varepsilon \sum_{i=1}^{m} s_i(a_i,y_i)$

z indywidualnymi funkcjami osiągnięcia postaci

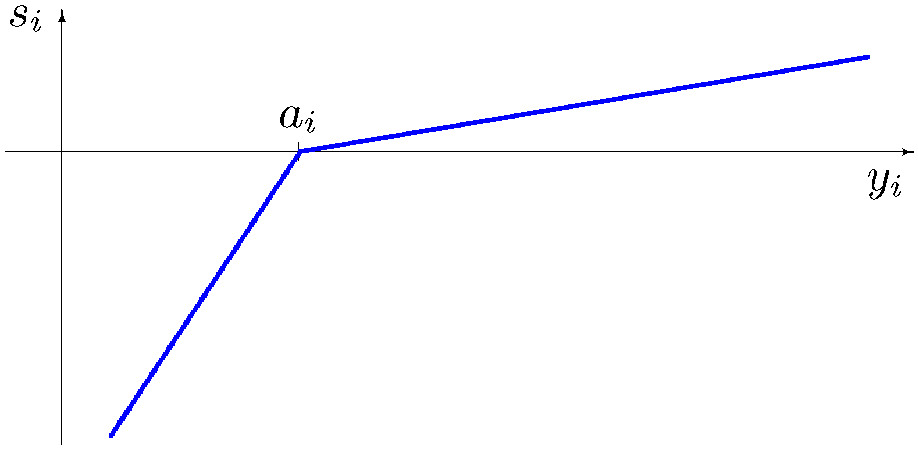
$s_i (a_i,y_i) = \left\{ \begin{array}{rl} \beta \lambda_i ( y_i - a_i ),\quad \mbox{jeśli} \quad y_i \ge a_i \\ \lambda_i ( y_i - a_i ),\quad \mbox{jeśli} \quad y_i < a_i\end{array} \right.,$

gdzie $\lambda_i$ są dodatnimi mnożnikami skalującymi, a $\beta$ jest małym parametrem dodatnim $0 < \beta < 1$.

Indywidualna funkcja osiągnięcia klasycznej wersji MPO

Zauważmy, że indywidualne funkcje osiągnięcia przesuwają początek układu współrzędnych w przestrzeni ocen do wektora poziomów aspiracji. Tym samym, przypisują miarę osiągnięcia 0 wartości oceny równej poziomowi aspiracji, ujemne miary osiągnięcia wartościom oceny poniżej poziomu aspiracji i dodatnie miary wartościom oceny przekraczającym poziom aspiracji. Następnie wszystkie oceny są przeskalowane za pomocą mnożników $\lambda_i$ dla znormalizowania ich zakresów zmienności. Dalej, wartości dodatnie wyrażające znormalizowane nadmiary wartości ocen ponad poziomy aspiracji są pomniejszane przez czynnik $\beta$. Najczęściej przyjmuje się $\beta$ rzędu $10^{-3}$. W konsekwencji przyrost wartości oceny ponad poziomem aspiracji powoduje znacznie mniejszy przyrost wartości funkcji osiągnięcia niż w przypadku nieosiągania poziomu aspiracji.

Maksymalizacja funkcji skalaryzującej na zbiorze ocen osiągalnych $A$ wyznacza niezdominowany wektor ocen ${\bf y}$ i generujące go rozwiązanie efektywne ${\bf x}$. Wyznaczone rozwiązanie efektywne zależy od wartości dwóch grup parametrów: poziomów aspiracji $a_i$ i czynników skalujących $\lambda_i$. Czynniki skalujące określają kierunek przechodzącej przez punkt odniesienia ${\bf a}$ prostej równych indywidualnych osiągnięć, wzdłóż której dokonuje się maksymalizacja regularyzowanej skalaryzacji maksyminowej.

Metoda punktu odniesienia nie traktuje wektora aspiracji jako bezwględnego celu a jedynie jako punkt odniesienia. Dlatego nawet w przypadku osiągalnego wektora aspiracji MPO wyznacza niezdominowany wektor ocen.