Podręcznik

Najbardziej znaną i najbardziej zbadaną grą o sumie zerowej jest gra w dylemat więźnia.

Dwóch podejrzanych zostało zatrzymanych przez policję. Policja, nie mając wystarczających dowodów do postawienia zarzutów, rozdziela więźniów i przedstawia każdemu z nich tę samą ofertę: jeśli będzie zeznawać przeciwko drugiemu, a drugi będzie milczeć, to zeznający wyjdzie na wolność, a milczący dostanie dziesięcioletni wyrok. Jeśli obaj będą milczeć, obaj odsiedzą 6 miesięcy za inne przewinienia. Jeśli obaj będą zeznawać, obaj dostaną pięcioletnie wyroki. Każdy z nich musi podjąć decyzję niezależnie i żaden nie dowie się, czy drugi milczy czy zeznaje, aż do momentu wydania wyroku. Jak powinni postąpić? (za Wikipedia: https://pl.wikipedia.org/wiki/Dylemat_więźnia).

Dla gry w dylemat więźnia, macierz wypłat przedstawia się następująco:

$q_x$	K milczy	K zeznaje
W milczy	-0,5; -0,5	-10; 0
W zeznaje	0;-10	-5; -5

Zastanówmy się, która decyzja dla Pani Kolumny i dla Pana Wiersza będzie najlepsza, najbardziej korzystna. Pierwszym pojęciem, które wprowadzimy będzie dominacja strategii.

Kolejnym pojęciem będzie strategia dominująca:

Na podstawie powyższych definicji, możemy zaproponować jeden ze sposobów wyznaczania rozwiązań gier o sumie niezerowej. Polega on na wyznaczeniu strategii zdominowanych dla każdego z graczy i rozgrywanie gry za ich pomocą. Niestety, takie strategie rzadko występują w rzeczywistych grach.

Kolejną definicją jest optymalność wyniku gry w sensie Pareto. 

Warto przedstawić także definicję nieoptymalności wyniku gry w sensie Pareto.

Z powyższych definicji możemy zdefiniować kryterium Pareto: tylko wynik optymalny w sensie Pareto może być akceptowalny jako rozwiązanie gry. Kryterium Pareto stanowi podstawową zasadę racjonalności grupowej. 

Sprawdźmy, czy rozwiązania gry w dylemat więźnia są optymalne w sensie Pareto. Naszkicujmy wszystkie rozwiązania tej gry w dwuwymiarowej przestrzeni wypłat:

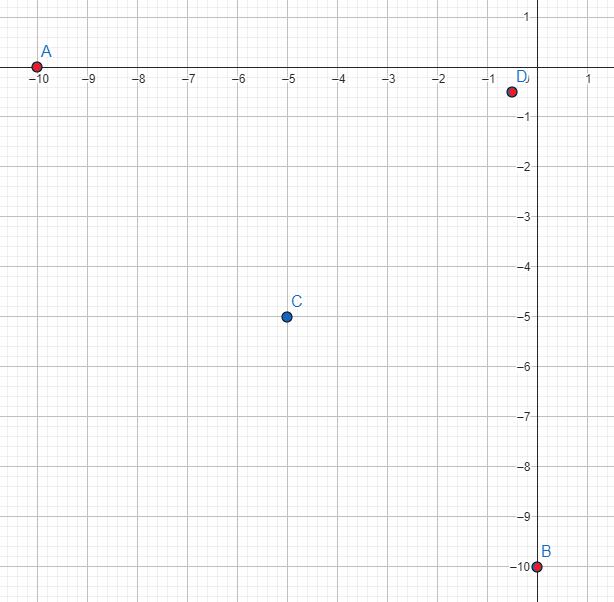
Wyniki gry, które są oznaczone czerwonym kolorem ($(W_m, K_m), (W_m, K_z), (W_z, K_m)$), są optymalne w sensie Pareto. Dalej, spełniają kryterium racjonalności grupowej. Spełnienie tego kryterium przez rozwiązanie gry powoduje, że gracz nie może zyskać więcej, bez spowodowania straty dla drugiego gracza. 

Poznaliśmy pojęcie strategii dominującej i możliwość (rzadką) na poszukiwanie rozwiązania gry. Poznaliśmy kryterium Pareto, które wskazuje racjonalne grupowo rozwiązania. Jednak poszukiwanie "dobrych" rozwiązań gry może zostać przeprowadzone przy użyciu tzw. koncepcji rozwiązania (ang. solution concept). Tworzy pewne założenia co do rozwiązania gry i formalnie tłumaczy ono  jak zostanie rozegrana gra. Większość koncepcji rozwiązania jest oparta o koncepcje równowagowe.

Najbardziej znana koncepcja rozwiązania została zaproponowana przez Johna Nasha w 1951 r. Zakłada ona, że w grze znajdującej się w równowadze żaden z graczy nie ma zachęt jednostronnie odstępować o strategii równowagii. Równowaga Nasha (w strategiach czystych) jest to taki profil strategii czystych $a^*\in A$, że dla każdego $i \in N$ i dla każdej strategii czystej $a_i$ gracza i-tego spełnia:

$u_i(a^*) = u_i(a_1^*, ..., a_i^*, ..., a_n^*) \geq  u_i(a_1^*, ..., a_i, ..., a_n^*)$

Nash udowonił, że każda skończona gra ma przynajmniej jeden punkt równowagi Nasha (niekoniecznie w strategiach czystych). Jednak w tym podręczniku nie będziemy zajmować się strategiami mieszanymi. 

Przeanalizujmy teraz grę w dylemat więźnia i pokażmy jedną z metod wyznaczania punktów równowagowych Nasha.

$q_x$	K milczy		K zeznaje
W milczy	-0,5; -0,5	$\rightarrow$	-10; 0
	$\downarrow$		$\downarrow$
W zeznaje	0;-10	$\rightarrow$	-5; -5

Rozpocznijmy naszą analizę do punktu $W_m, K_m$. Czy Pan Wiersz ma zachęty do jednostronnej zmiany swojej decyzji W obecnej sytuacji jego wypłata wynosi -0.5, przy zmianie decyzji na $W_z$ otrzymały on większą wypłatę równą 0. Wobec tego Pan Wiersz ma jednostonną zachętę na zmianę decyzji. Jest to oznaczane strzałką. Obecnie znajdujemy się w punkcie $W_z, K_m$, przeanalizujmy czy Pani Kolumnie opłaca się jednostronnie zmienić strategię. Obecnie jej wypłata jest równa -10, zaś przy zmianie jej strategii na $K_z$ jej wypłata rośnie do -5. Zatem Pani Kolumna ma zachętę do jednostronnej zmiany decyzji, co znowu oznaczone jest strzałką. Teraz jesteśmy w punkcie $W_z, K_z$, sprawdźmy teraz, czy Panu Wierszowi opłaci się jednostronnie zmienić swoją decyzję na $W_m$. Jego obecena wypłata to -5, po zmianie decyzji wynosi ona -10. Wobec tego, Panu Wierszowi (ani Pani Kolumnie) nie opłaca się jednostronnie zmienić swojej decyzji, co oznacza, że punkt $W_z, K_z$ jest punktem równowagi Nasha.