Podręcznik

• Zmienne decyzyjne: $x_j = 1,2,...,n$
• Przestrzeń decyzji: $X = R^n$
• Zbiór decyzji dopuszczalnych: $Q\subset X$
  
• Wektory (rozwiązania, decyzje) dopuszczalne: $x\in Q$
• Miara jakości (wynik) decyzji, funkcja celu, kryterium: $f: R^n\rightarrow R$
•  Zadanie optymalizacji (programowanie matematyczne):\\
     $\max \{ f(x): x\in Q\}$

        Wyznaczyć $\bar{x}\in Q$ taki, że
        $f(\bar{x}) \geq f(x)\quad \forall x\in Q$

•   $\bar{x}$ -- rozwiązanie optymalne
• $f(\bar{x})$ -- wartość optymalna

W zadaniach liniowych Q jest zbiorem rozwiązań następującego układu ograniczeń:

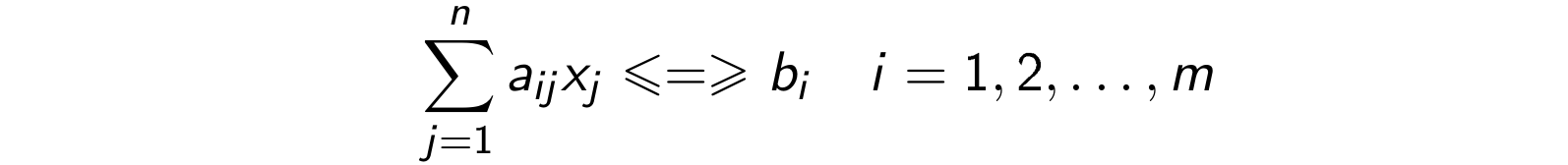
a funkcja celu ma postać:

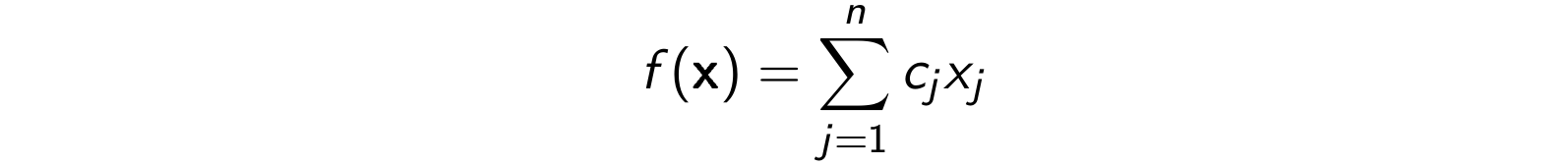
W problemach dyskretnych natomiast zbiór $Q$ jest dyskretny, tzn. jest zbiorem skończonym albo jest skończoną sumą niespójnych składowych. Oznacza to, że zmienne decyzyjne przyjmują wartości całkowitoliczbowe. W takiej sytuacji zadanie optymalizacji, liniowe-całkowitoliczbowe (PLC, ILP), wygląda (w zapisie macierzowym) następująco:

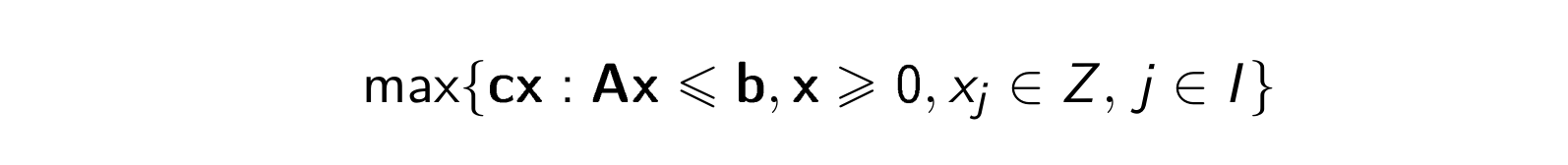
Jeśli w zadaniu mogą występować również zmienne ciągłe, mamy do czynienia z zadaniem mieszanym, liniowym-całkowitoliczbowym (MILP).

Znaczenie problemów MILP wynika z tego, że wiele zagadnień nieliniowych, kombinatorycznych czy logicznych daje się modelować dokładnie bądź w przybliżeniu za pomocą takich modeli. W szczególności modelowanie matematyczne, w tym MILP, możemy traktować jako rodzaj programowania deklaratywnego, analogicznie do języka opisu zapytań SQL. Stąd nazwa programowanie matematyczne.

Przykłady klas problemów, które można rozwiązywać przez optymalizację modeli MILP: zadania harmonogramowania, kombinatoryczne, przydziału zasobów, optymalizacji łańcucha dostaw, optymalizacji sieciowej, etc.

Modele MILP mogą być rozwiązywane za pomocą specjalizowanych algorytmów (branch-and-bound, branch-and-cut, programowanie dynamiczne, itp), często dostępnych w postaci solwerów. Do najbardziej znanych należą: a)komercyjne: CPLEX, GUROBI b) otwarte: CBC, GLPK, ORTOOLS.