Podręcznik

Czasami konieczne jest zamodelowanie zachowania zmiennej binarnej tak, aby przyjmowała ona wartość 1 jeśli pewna inna zmienna lub wyrażenie są dodatnie. Taka zmienna binarna jest nazywana flagą dodatniości.

Niech zmienna ciągła  \(x\) będzie ograniczona w przedziale wartości: \(0\leq x \leq M\). Niech także dana będzie zmienna binarna $u\in\{0,1\}\). Warunek  \(u=1\) wtedy gdy \(x > 0\) osiągniemy stosując następujące nierówności:

A w przypadku wyrażenia (przykładowo wyrażenia liniowego):

Przykładowo, koszt transportu w zadaniu transportowym, uwzględniający tzw koszt stały, czyli koszt niezależny od ilości przewożonego towaru, naliczany jeśli ilość przewożonego towaru jest niezerowa:

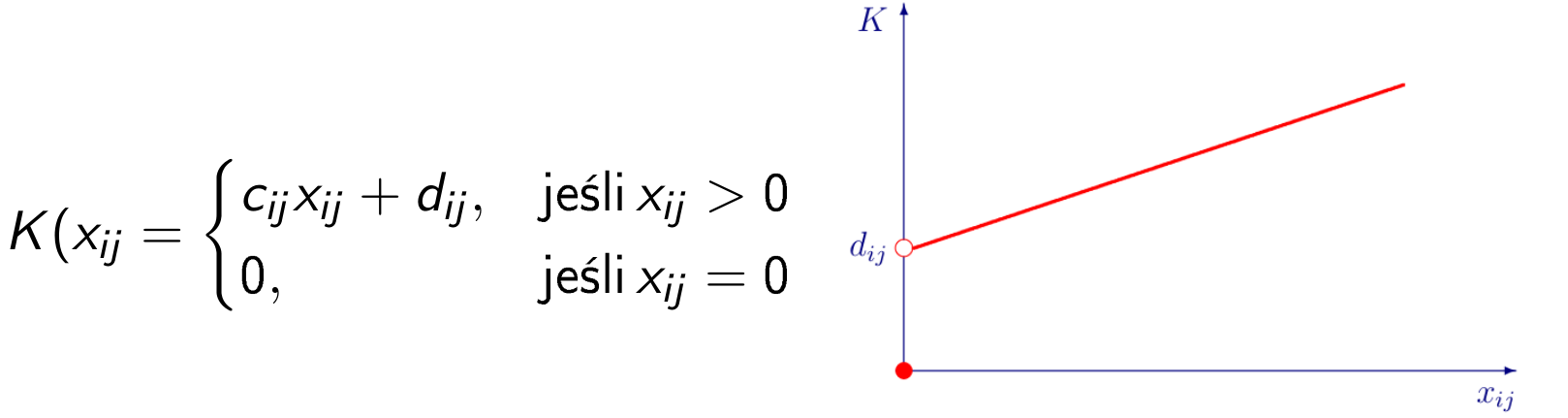
Model mieszany, liniowy-całkowitoliczbowy, zadania transportowego z takim kosztem będzie następujący:

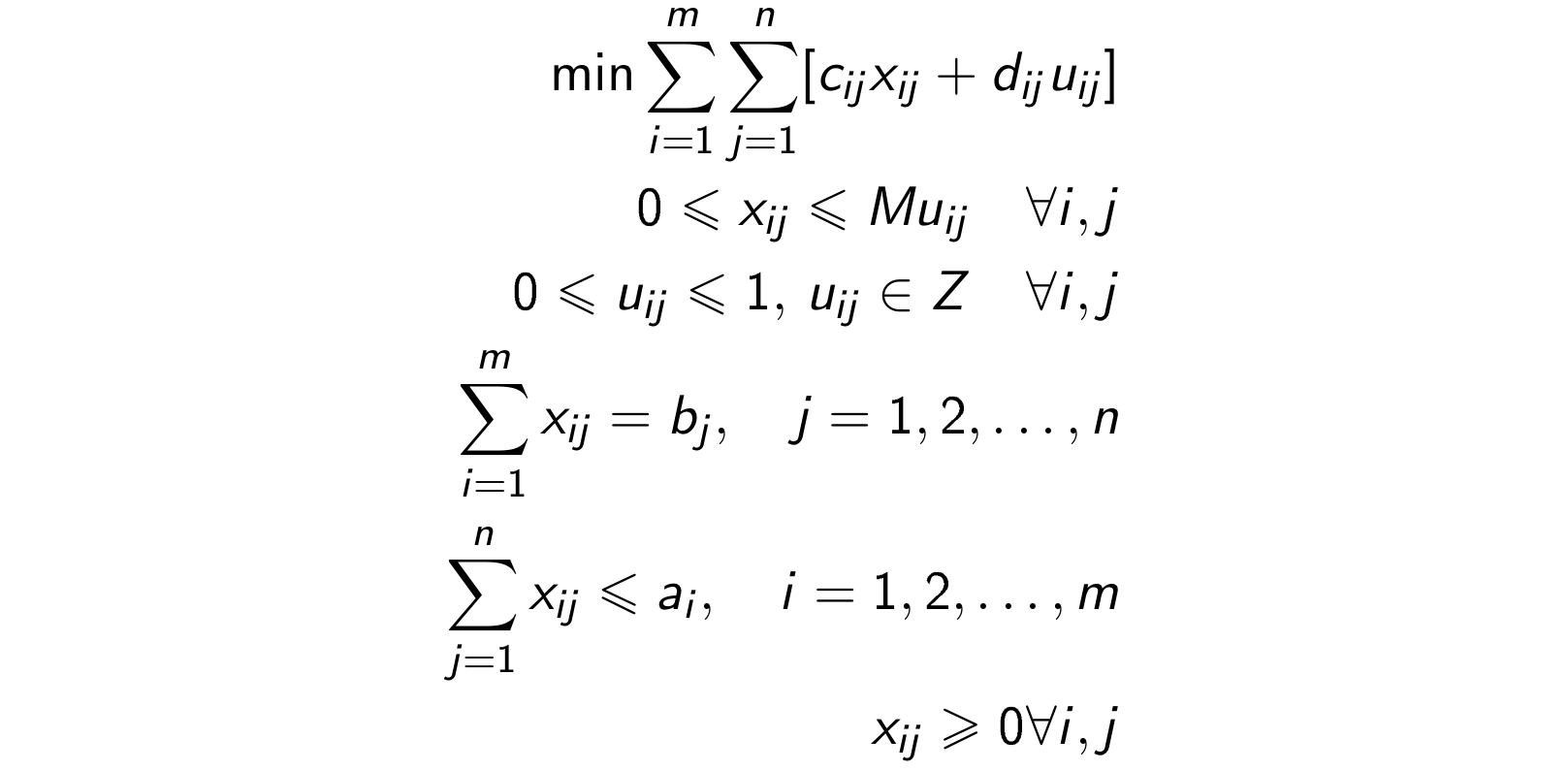
Stosując podobne techniki możemy ograniczyć liczbę zmiennych dodatnich, tzn. co najwyżej \(k\) zmiennych \(x_j\) przyjmie wartości dodatnie:

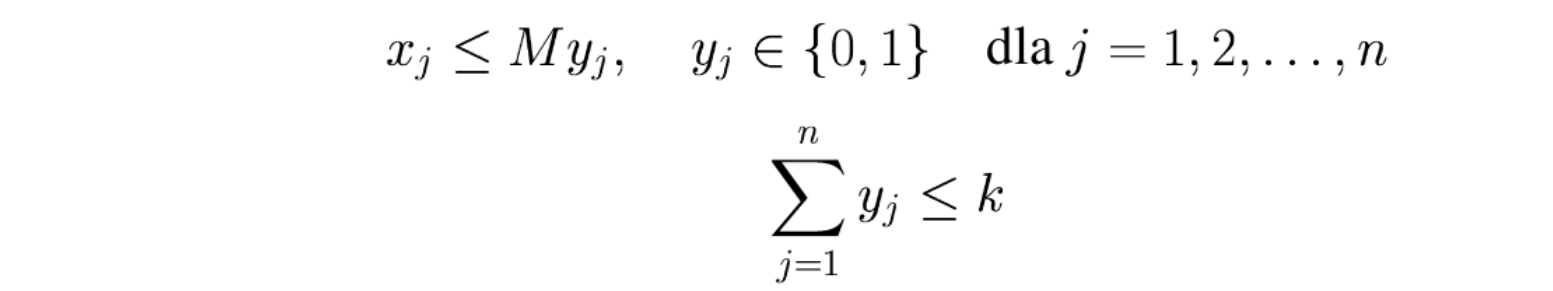
Ponownie przykład zadania transportowego, w którym co najwyżej \(k\) dostawców realizuje zapotrzebowanie odbiorcy \(j\):

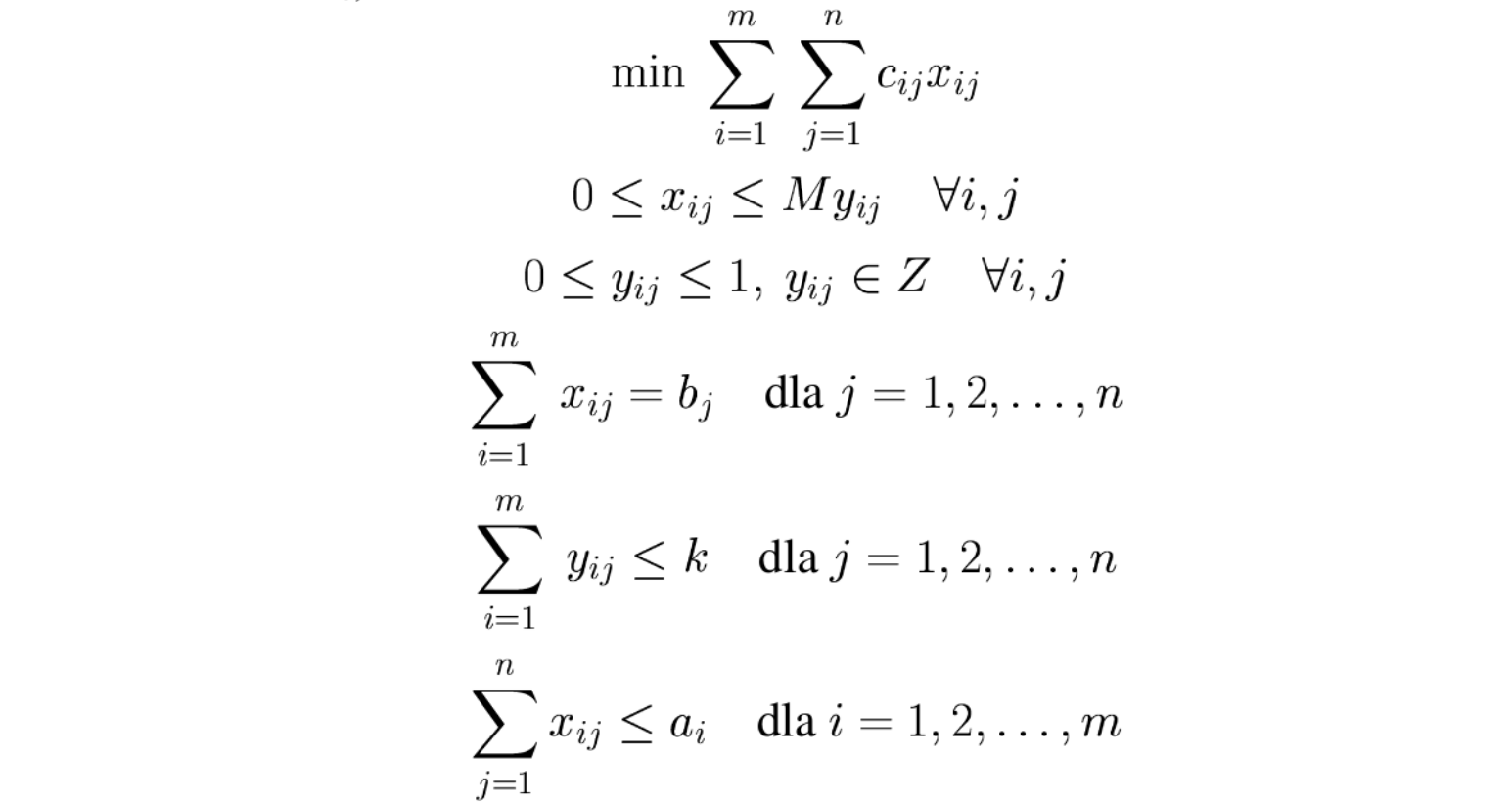
Analogicznie do ograniczenia liczby zmiennych dodatnich możemy wyrazić ograniczoną liczbę naruszonych warunków, czyli niespełnionych ograniczeń. Precyzyjnie, w układzie \(m\) nierówności:

co najmniej \(k\) warunków musi być spełnionych, a pozostałe \(m-k\) nie muszą być spełnione.

Osiągniemy to następującym modelem całkowitoliczbowym:

Rozszerzając ten model możemy maksymalizować liczbę spełnionych warunków:

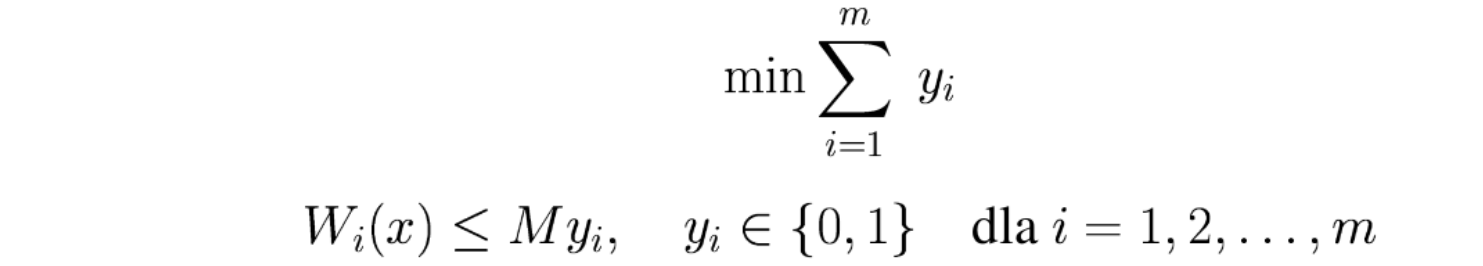
przy czym funkcja celu oznacza liczbę niespełnionych warunków.