Podręcznik

Rozważmy następujące zadanie modelowania.

Zadanie 1. 

Rozważana jest hodowla ryb. Trzy gatunki ryb mogą być hodowane w dwóch stawach o różnych rozmiarach. Staw 1 mieści maksymalnie 120 ton ryb, a staw 2 – 150 ton ryb. Narybek jest kupowany w cenie, odpowiednio, 2, 2.5, 3 tyś.zł za kilogram. W czasie hodowli ryby pierwszego i drugiego gatunku powiększają swoją masę, odpowiednio, 80 i 100 razy niezależnie tego, w którym stawie się znajdują. Natomiast ryby trzeciego gatunku powiększają swoją masę 130 razy w stawie 1 i 120 razy w stawie 2. Ryby gatunku 2 i 3 nie mogą przebywać razem w jednym stawie. Cena sprzedaży 1 kg ryby wynosi, odpowiednio, 15, 18, 14 zł. Zaplanować hodowlę przynoszącą największy zysk (koszty paszy są pomijane). Sformułować model programowania mieszanego liniowego–całkowitoliczbowego realizujący to zadanie.

Rozwiązanie.

zmienne
$x_{ij}$ - ilość narybku gatunku i  w stawie j [kg]
$v_{ij}$ - zmienna binarna = 1 jeśli narybek i jest w stawie j

$M$ - duża stała

ograniczenie zapewniające odpowiednie ustawienie zmiennej v jeśli zmienna x jest dodatnia
$\forall i,j     x_{ij} \leq M v_{ij}$

maksymalna pojemność stawów (ilość narybku mnożona przez współczynniki wzrostu)
$80*x_{11}+100*x_{21}+130*x_{31}$
$80*x_{12}+100*x_{22}+120*x_{32}$

gatunek drugi i trzeci nie mogą przebywać w tym samym stawie
$v_{21}+v_{31}$
$v_{22}+v_{32}$

Funkcja celu
max
$15*80*(x_{11}+x_{12}) + 18*100*(x_{21}+x_{22}) + 14*(130*x_{31}+120*x_{32})$ // przychód ze sprzedaży
$-2000*(x_{11}+x_{12})-2500*(x_{21}+x_{22})-3000*(x_{31}+x_{32})$  // koszt zakupu narybku

Zadanie 2.

Dwa węzły sieci internet są połączone z dwoma miastami (każdy z każdym). Aktualne przepustowości łączy wynoszą [Gb]:

W1->M1: 1.5, W1->M2: 0.8, W2->M1: 2.1, W2->M2: 0.9.

Prognozy przewidują, że ruch wzrośnie i miasto pierwsze będzie generowało sumaryczny ruch na poziomie 6.5Gb, a miasto drugie 3.6Gb. Przepustowość danego łącza można powiększyć o wielokrotność 1Gb po ustalonej cenie innej dla każdego łącza [tyś. zł/Gb]:

W1->M1: 180, W1->M2: 120, W2->M1: 160, W2->M2: 150.

Samo rozpoczęcie inwestycji na danym łączu generuje następujący koszt [tyś. zł]:

W1->M1: 250, W1->M2: 250, W2->M1: 320, W2->M2: 200.

Zaplanować inwestycję pokrywającą prognozowany ruch obydwu miast. Sformułować model programowania mieszanego liniowego–całkowitoliczbowego realizujący to zadanie.

Zadanie 3.

Dana jest krzywa ładowania, modelowana za pomocą krzywej schodkowej.

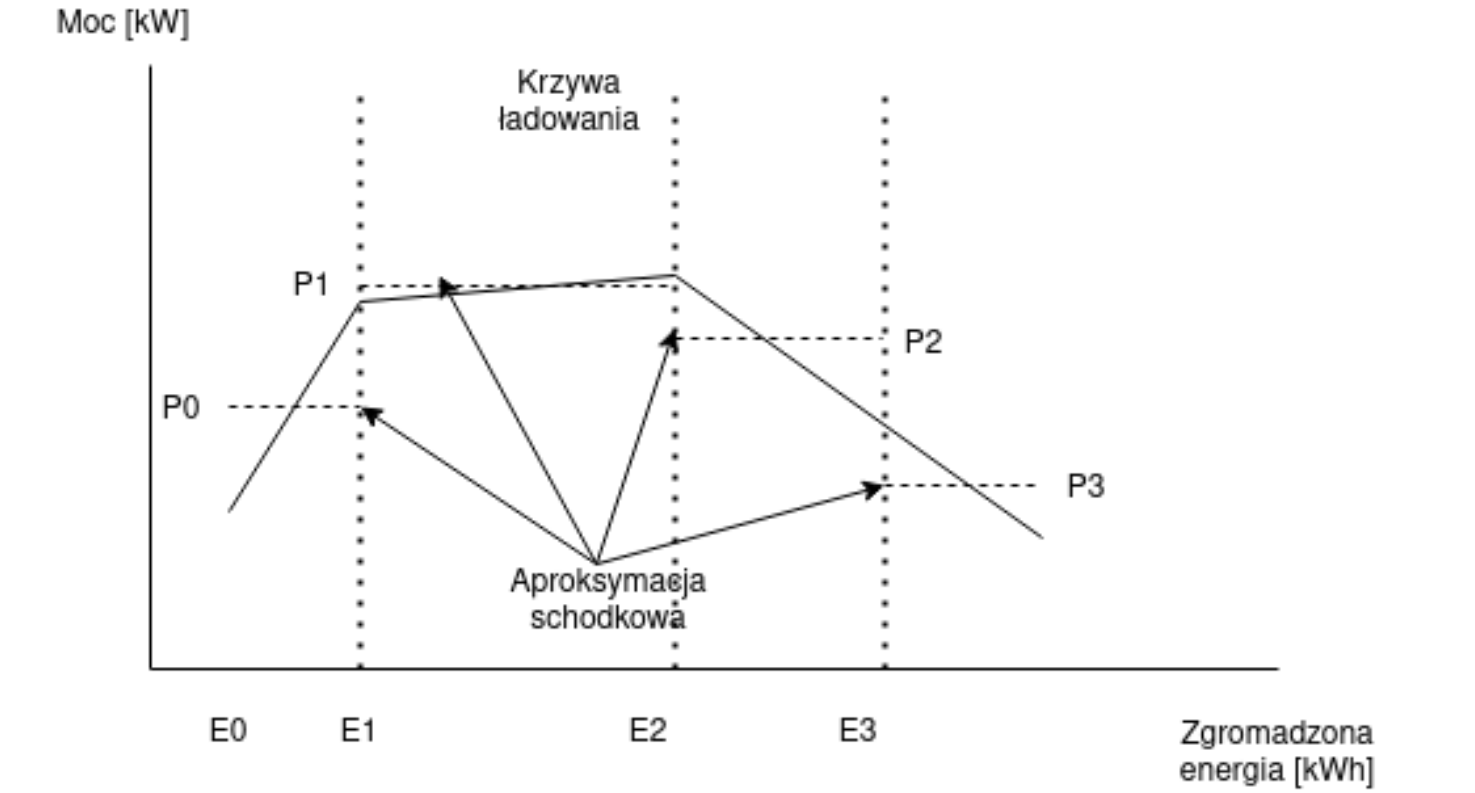
Wartości schodków są parametrami modelu i spełniają zależność:
$p_0 \leq p_1 \geq p_2 \geq p_3$.

Należy stworzyć model MILP, który prawidłowo wyznaczy wartość zmiennej oznaczającej czas ładowania (ozn. $dt$, jeśli poziom naładowania akumulatora przed ładowaniem jest dany w postaci zmiennej (ozn. $tank$) i a ilość ładowanej na stacji energii również jest dana w postaci zmiennej (ozn. $charge$). Zakładamy, że czas ładowania $dt$ jest minimalizowany.

Można przyjąć pewne nieścisłości modelu (sensowne). Generalnie liczba zmiennych binarnych powinna być jak najmniejsza. Model należy przetestować, np w środowisku AMPL.

Należy mieć na względzie, że powyższy model jest częścią większego modelu, np optymalizującego plan ładowania pojazdu na wielu stacjach.