Podręcznik

Jednym z głównych powodów implementacji drzew binarnego wyszukiwania (BST) jest jego zdolność do szybkiego oraz efektywnego wyszukiwania danych. Dzięki unikalnej strukturze drzewa BST, która opiera się na zasadzie porządkowania elementów wszystkie wartości w lewym poddrzewie są mniejsze, a w prawym większe niż wartość węzła. Dzięki temu możliwe jest szybkie odnalezienie poszukiwanego elementu poprzez kolejne porównania, podobnie jak w wyszukiwaniu binarnym.

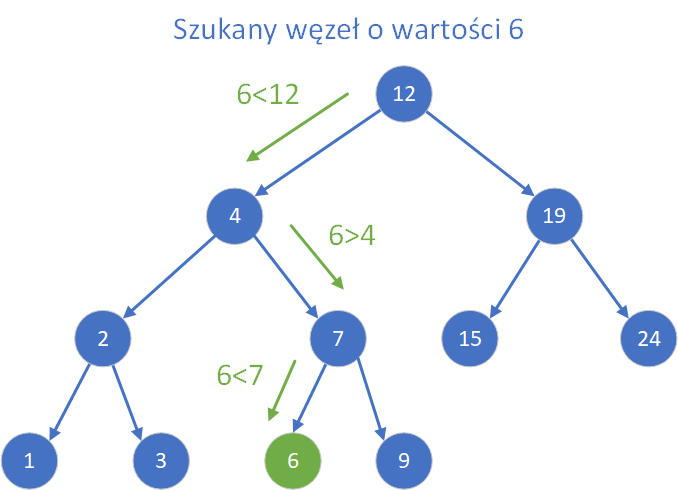
Proces wyszukiwania rozpoczyna się od korzenia drzewa. Jeśli wartość, której szukamy jest równa wartości w korzeniu, operacja kończy się sukcesem. W przeciwnym razie, jeśli szukana wartość jest mniejsza, algorytm przechodzi do lewego poddrzewa, natomiast jeśli większa to do prawego. Proces ten jest powtarzany rekurencyjnie lub iteracyjnie aż do momentu znalezienia wartości albo dotarcia do pustego wskaźnika (braku potomka), co oznacza, że dana wartość nie istnieje w drzewie. Poniżej na rysunku pokazano wyszukiwanie węzła o wybranej wartości na drzewie BST.

Poniżej przedstawiono kod aplikacji do wyszukiwania węzłów o podanej wartości w drzewie BST.

Node* searchRecursive(Node* root, int target) {
    if (root == nullptr || root->key == target)
        return root;
    if (target < root->key)
        return searchRecursive(root->left, target);
    else
        return searchRecursive(root->right, target);
}

Ta wersja funkcji działa rekurencyjnie, czyli wywołuje samą siebie, dopóki nie znajdzie szukanego elementu lub nie dojdzie do pustego wskaźnika (NULL), co oznacza, że elementu nie ma w drzewie. Jeśli bieżący węzeł jest pusty (NULL) lub zawiera szukaną wartość, zwracamy go. Jeśli szukana wartość jest mniejsza, kontynuujemy w lewym poddrzewie. Jeśli większa  w prawym poddrzewie.