Podręcznik

Operacje na drzewach AVL są podobne do tych w klasycznym drzewie BST (binarnego drzewa wyszukiwania), ale z dodatkowym warunkiem: po każdej operacji drzewo musi pozostać zrównoważone. AVL gwarantuje, że różnica wysokości lewego i prawego poddrzewa dla każdego węzła nie przekroczy 1, co zapewnia logarytmiczną złożoność operacji.

Operacja wstawiania wartości do drzewa AVL

Pierwszym krokiem algorytmu jest klasyczne przeszukiwanie drzewa BST w celu znalezienia odpowiedniego miejsca dla nowego węzła. W trakcie wykonywania operacji porównywana jest wartość nowego wierzchołka z wartościami już istniejącymi. Schodzi się w dół drzewa aż do miejsca w którym można bez naruszenia zasad BST wstawić nowy element. Proces ten nie różni się niczym od zwykłego wstawiania węzła do drzewa binarnego.

Po umieszczeniu nowego wierzchołka w odpowiednim miejscu, algorytm nie kończy działania, lecz zaczyna wracać w górę drzewa po tej samej ścieżce, którą schodził, aktualizując po drodze tzw. współczynniki wyważenia węzłów (oznaczane zwykle jako ww lub balance factor). Ten współczynnik odzwierciedla różnicę wysokości między lewym a prawym poddrzewem danego węzła i może przyjmować wartości od –1 do 1 w przypadku drzewa AVL, bez naruszenia jego struktury. Mamy wtedy kilka możliwości:

• współczynnik wyważenia jakiegoś węzła przyjmie wartość 0, oznacza to, że jego poddrzewa pozostały zrównoważone i ich wysokość się nie zmieniła. W takiej sytuacji nie ma potrzeby dalszego działania i algorytm kończy się, ponieważ nie doszło do naruszenia równowagi.
• współczynnik wyważenia staje się równy 1 lub –1, to wskazuje, że jedno z poddrzew stało się wyższe o jeden poziom, ale nadal całość spełnia warunki drzewa AVL. W takim przypadku kontynuujemy śledzenie ścieżki w górę do korzenia, ponieważ równowaga mogła zostać zachwiana wyżej w drzewie.
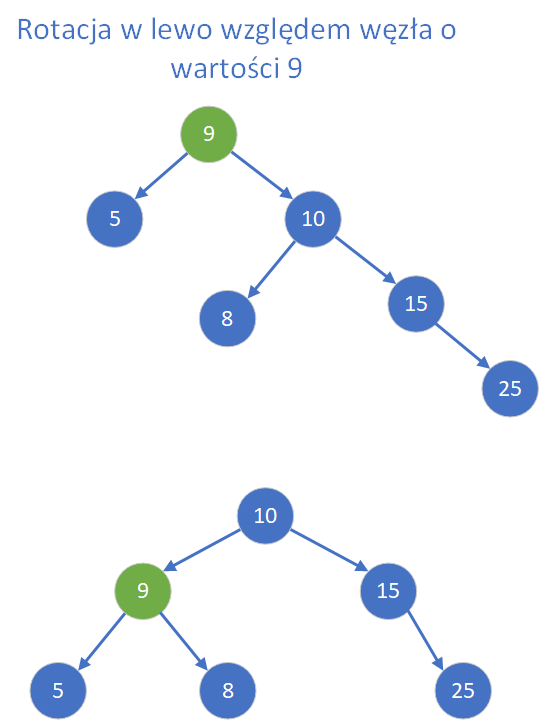
• współczynnik osiąga wartość 2 lub –2, oznacza to, że dane poddrzewo straciło wyważenie – różnica wysokości między jego lewym i prawym poddrzewem przekroczyła dopuszczalny próg. Wówczas należy zastosować odpowiednią rotację w celu przywrócenia równowagi. W zależności od kierunku wzrostu drzewa (czy nadmiar występuje po lewej, czy po prawej stronie, oraz w którym kierunku został dodany nowy wierzchołek), wykonuje się rotację pojedynczą (lewo-lewo lub prawo-prawo) albo podwójną (lewo-prawo lub prawo-lewo).

Poniżej przedstawiono przykład rysunkowy rotacji drzewa lewo względem korzenia.

Operacja wstawiania wartości do drzewa AVL

Analogicznie do operacji wstawiania, również operacja usuwania wierzchołka z drzewa AVL składa się z kilku logicznych kroków, których celem jest zachowanie zarówno poprawnej struktury drzewa BST, jak i zrównoważenia AVL. Różnica polega na tym, że w usuwaniu wprowadzana jest potencjalna redukcja wysokości drzewa, co również może prowadzić do naruszenia równowagi. 

Pierwszym krokiem algorytmu jest klasyczne przeszukiwanie drzewa BST w celu znalezienia wierzchołka, który ma zostać usunięty. Przechodząc przez kolejne węzły, porównywana jest wartość klucza docelowego z bieżącym węzłem i odpowiednio schodzi się w dół do lewego lub prawego poddrzewa, aż zostanie znaleziony wierzchołek o poszukiwanej wartości. Ta część procesu nie różni się niczym od usuwania elementu w zwykłym drzewie BST.

Gdy zostanie odnaleziony węzeł do usunięcia, algorytm rozpoznaje jeden z trzech przypadków:

• węzeł nie ma dzieci - zostaje po prostu usunięty. 
• węzeł ma jedno dziecko - dziecko zastępuje węzeł w jego miejscu. 
• węzeł ma dwóch potomków, węzeł zostaje zastąpiony przez następnika (najmniejszy węzeł w prawym poddrzewie) lub poprzednika (największy węzeł w lewym poddrzewie), a jego oryginalna pozycja zostaje fizycznie usunięta w sposób analogiczny do poprzednich przypadków. 

Po wykonaniu rzeczywistego usunięcia, algorytm zaczyna wracać w górę drzewa dokładnie po ścieżce, którą wcześniej schodził i aktualizuje współczynniki wyważenia każdego napotkanego węzła. W tym momencie wierzchołki mogą ulec przechyłowi w przeciwnym kierunku niż podczas wstawiania, ponieważ wysokość któregoś z poddrzew się zmniejszyła. Podobnie jak wcześniej, pojawiają się trzy możliwości:

• współczynnik wyważenia jakiegoś węzła przyjmie wartość 0, oznacza to, że jego poddrzewa pozostały zrównoważone i ich wysokość się nie zmieniła. W takiej sytuacji nie ma potrzeby dalszego działania i algorytm kończy się, ponieważ nie doszło do naruszenia równowagi.
• współczynnik wyważenia staje się równy 1 lub –1, to wskazuje, że jedno z poddrzew stało się wyższe o jeden poziom, ale nadal całość spełnia warunki drzewa AVL. W takim przypadku kontynuujemy śledzenie ścieżki w górę do korzenia, ponieważ równowaga mogła zostać zachwiana wyżej w drzewie.
• współczynnik osiąga wartość 2 lub –2, oznacza to, że dane poddrzewo straciło wyważenie – różnica wysokości między jego lewym i prawym poddrzewem przekroczyła dopuszczalny próg. Wówczas należy zastosować odpowiednią rotację w celu przywrócenia równowagi. W zależności od kierunku wzrostu drzewa (czy nadmiar występuje po lewej, czy po prawej stronie, oraz w którym kierunku został dodany nowy wierzchołek), wykonuje się rotację pojedynczą (lewo-lewo lub prawo-prawo) albo podwójną (lewo-prawo lub prawo-lewo).