Podręcznik

Algorytmy gradientowe są istotną klasą algorytmów optymalizacji wykorzystywaną szeroko w uczeniu sieci neuronowych. Celem optymalizacji jest dobór parametrów modelu, tak, aby zminimalizować funkcję kosztu. Funkcja kosztu opisuje błąd popełniany przez model dla przykładów ze zbioru uczącego i chcemy ją zmniejszać. Konkretne wzory na funkcje kosztu w różnych zastosowaniach omówimy w rozdziale 3.4.

W podstawowej wersji algorytm minimalizacji metodą spadku działa następująco. Wariant ten nazywamy metodą gradientu prostego:

1. ustaw wartość początkową $w$ na $w_0$

2. dopóki nie warunek stopu $w \gets w - \alpha \frac{\partial J}{\partial w}$

3. idź do 2.

Poprzez $w$ oznaczamy parametry naszego modelu (np. wagi sieci neuronowej). Może to być pojedyncza liczba, ale najczęściej jest to wektor lub macierz wielu liczb. Algorytm rozpoczynamy od przypisania wartości początkowej $w_0$. Następnie wyznaczamy gradient funkcji kosztu $J$ po parametrach $\frac{\partial J}{\partial w}$ i modyfikujemy wartości $w$ według wzoru $w \gets w - \alpha \frac{\partial J}{\partial w}$. $\alpha$ nazywamy współczynnikiem uczenia. Jest to niewielka liczba dodatnia określająca wielkość kroków wykonywanych przez algorytm. Zapętlamy ten krok aż do osiągnięcia warunku stopu.

Warunkiem stopu może być:

• Wykonanie określonej liczby iteracji lub przekroczenie czasu obliczeń. Warunek ten odnosi się do wykorzystania zasobów obliczeniowych.

• Osiągnięcie wystarczająco małej wartości funkcji kosztu $J$. Warunek ten odnosi się do uzyskania zakładanej jakości modelu. Zamiast funkcji kosztu można wykorzystać inną metrykę. Dla uniknięcia zjawiska przeuczenia, zalecane jest wykonywanie sprawdzenia na zbiorze walidacyjnym.

• Brak poprawy funkcji kosztu w kolejnych iteracjach. Warunek ten odnosi się do braku perspektyw na dalszą poprawę rozwiązania. Dla uniknięcia zjawiska przeuczenia, zalecane jest wykonywanie sprawdzenia na zbiorze walidacyjnym.

• Osiągnięcie odpowiednio małej wartości modułu gradientu $\frac{\partial J}{\partial w}$. Małe wartości modułu gradientu oznaczają małe kroki algorytmu. Warunek ten odnosi się do braku perspektyw na dalszą poprawę rozwiązania.

Rozważmy zestaw przykładów dla wypukłej funkcji kosztu i jednowymiarowego $w$ przedstawiony na rysunku 2. Funkcja ta ma jedno globalne minimum dla wartości $w^* = 5$ i $J(5) = 1$.

(a) Gradienty

(b) $\alpha = 0.1$

(c) $\alpha = 0.03$

(d) $\alpha = 0.9$

(e) $\alpha = 1.1$

(f) Funkcja kosztu $\alpha = 0.1$

Rysunek 2: Optymalizacja metodą spadku gradientu.

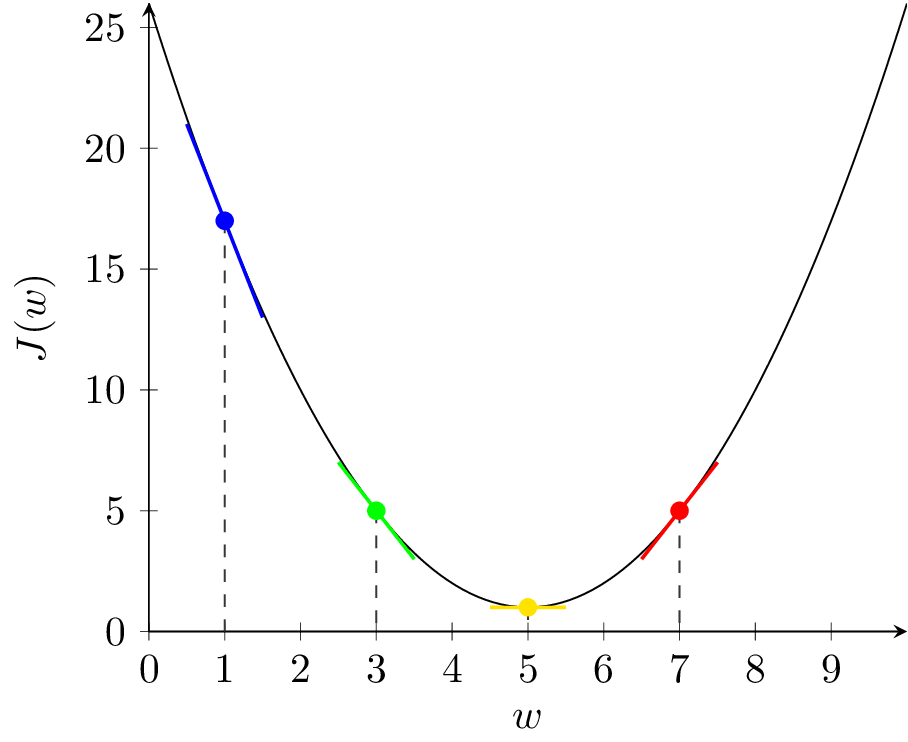
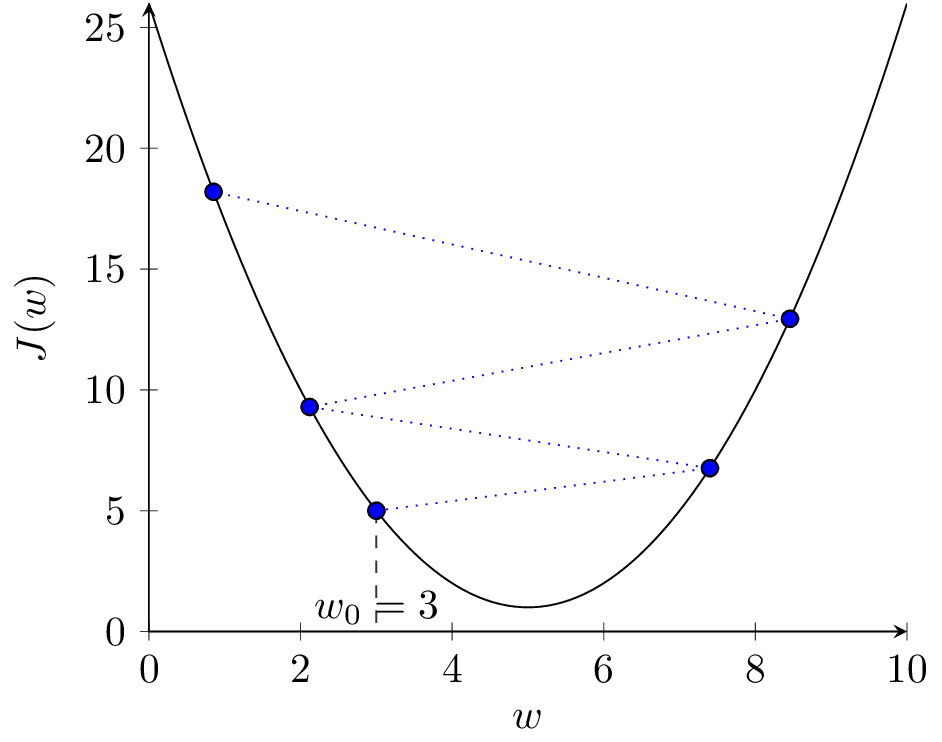
Pochodna $\frac{\partial J}{\partial w}$ jest współczynnikiem kierunkowym prostej stycznej do wykresu funkcji $J(w)$. Na rysunku 2(a), w punkcie niebieskim pochodna $\frac{\partial J}{\partial w}$ ma wartość ujemną. Zatem $- \alpha \frac{\partial J}{\partial w}$ ma wartość dodatnią i kolejnym kroku zwiększymy wartość $w$ (przesuniemy się w prawo). Jest to działanie prawidłowe, ponieważ znajdujemy się w punkcie $w = 1$ i zwiększanie przybliża nas do optymalnej wartości $w^* = 5$. Analogicznie wygląda sytuacja dla punktu zielonego, tylko nachylenie stycznej (pochodna) jest mniejsze, więc algorytm wykona mniejszy krok (mniej zwiększy wartość $w$). Odwrotnie, dla punktu czerwonego, pochodna jest dodatnia, więc $- \alpha \frac{\partial J}{\partial w}$ ma wartość ujemną i w kolejnym kroku zmniejszymy wartość $w$. Również jest to działanie prawidłowe. Punkt żółty znajduje się w optimum i pochodna wynosi zero. Jeśli trafimy w ten punkt, algorytm się zatrzyma.

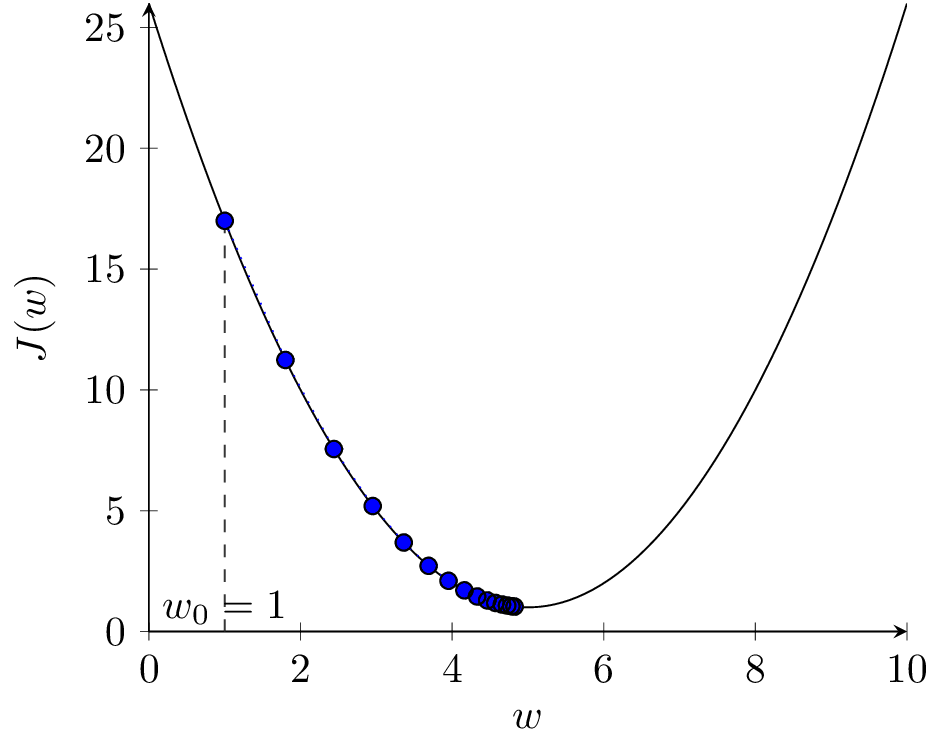
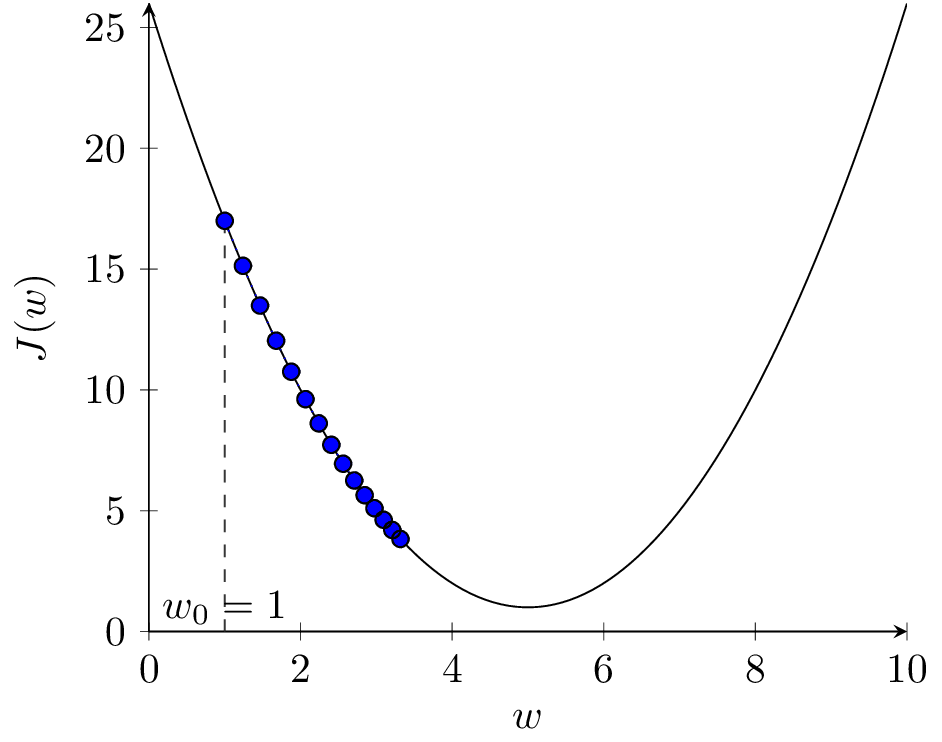
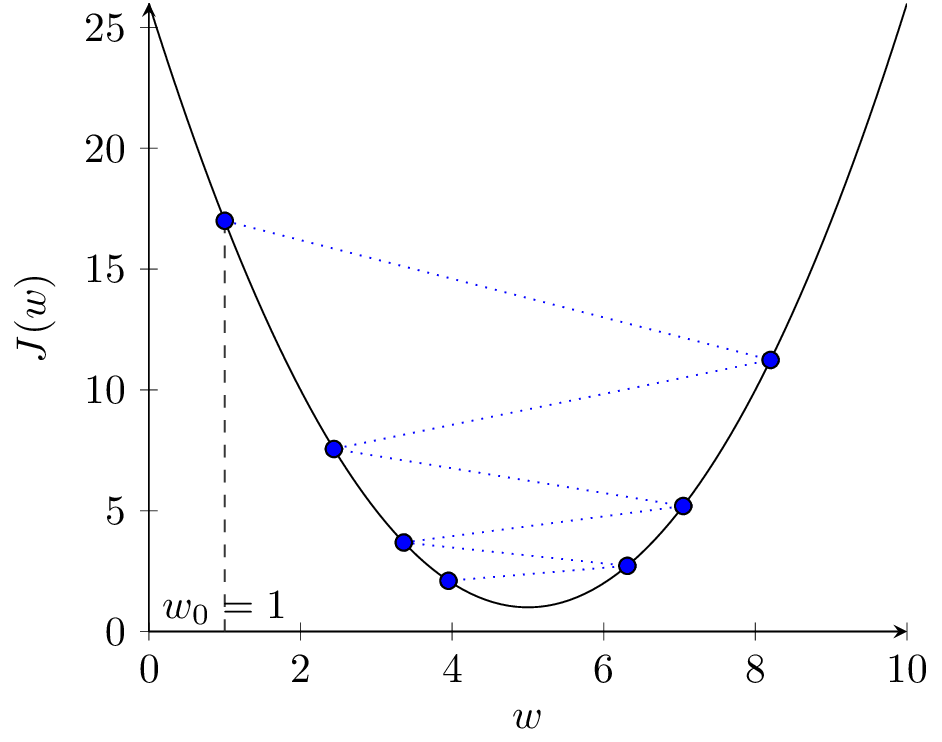
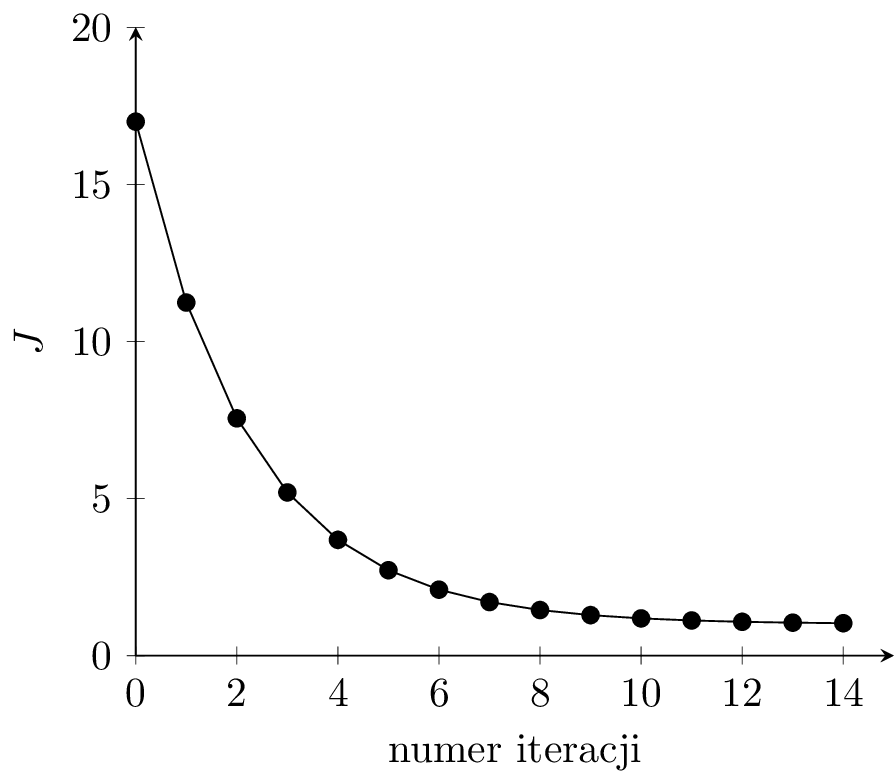
Na rysunku 2(b) przedstawione zostały kolejne kroki algorytmu dla $\alpha = 0.1$. Widzimy, że po 15 iteracjach algorytm znajduje się bardzo blisko optimum. Dla mniejszej wartości $\alpha = 0.03$ (rys. 2(c)) algorytm porusza się dobrym kierunku, ale wolniej. Dla większej wartości $\alpha = 0.9$ (rys. 2(d)) algorytm zaczyna przeskakiwać z jednej strony minimum na drugą, funkcja kosztu się zmniejsza, ale algorytm staje się mniej stabilny. Dalsze zwiększanie $\alpha$ do wartości 1.1 prowadzi do sytuacji jak na rysunku 2(e). Kroki algorytmu są za duże, funkcja kosztu zwiększa wartość w kolejnych krokach, algorytm jest rozbieżny.

Wartość współczynnika uczenia $\alpha$ jest jednym z hiper-parametrów w uczeniu sieci neuronowych i ma istotne znaczenie dla działania algorytmu.

Na rysunku 2(f) widzimy wykres wartości funkcji kosztu w kolejnych iteracjach dla $\alpha = 0.1$. Dla prawidłowo przebiegającego procesu uczenia funkcja kosztu powinna spadać w kolejnych iteracjach uczenia dla zbioru uczącego. Jeśli model zacznie się przeuczać, to koszt dla zbioru walidacyjnego w pewnym momencie może zacząć rosnąć. Jest to znak, że powinniśmy przerwać uczenie.