Podręcznik: Neuron

3. Perceptron wielowarstwowy

3.1. Neuron

Przyjrzyjmy się teraz jak działa pojedynczy neuron (rysunek 4).

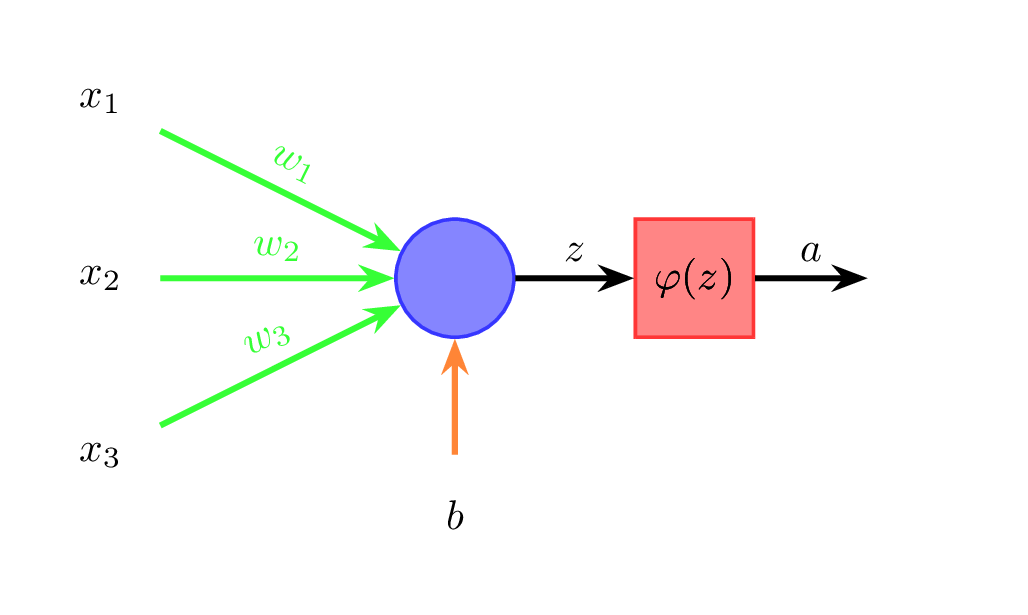
Schemat działania pojedynczego neuronu z wejściami x1, x2, x3, wagami w1, w2, w3, wyrazem wolnym b i funkcją aktywacji

Rysunek 4: Neuron (perceptron). Schemat został przygotowany z pomocą modelu GPT-4 (https://openai.com/gpt-4)

Dane wejściowe (na rysunku $x_1$ , $x_2$ , $x_3$ ) mnożone są przez odpowiednie wagi ( $w_1$ , $w_2$ , $w_3$ ) i sumowane. Do sumy dodawany jest jeszcze wyraz wolny $b$ (ang. bias) (wzór 1):

$z = w_1 x_1 + \ldots + w_n x_n + b$

Do otrzymanej sumy $z$ stosowana jest funkcja aktywacji $\varphi$ (wzór 2):

$a = \varphi(z)$

Wyjście neuronu oznaczamy poprzez $a$ . W perceptronie wielowarstwowym wyjścia neuronów warstwy poprzedniej stają się wejściami neuronów warstwy kolejnej. Każda strzałka pomiędzy neuronami na rysunku 3 ma przypisaną wagę, a każdy neuron ma przypisany wyraz wolny.

Analogie biologiczne

Działanie perceptornu ma pewne podobieństwa do neuronów biologicznych. Biologiczny neuron jest układem o wielu wejściach (dendryty) i jednym wyjściu (akson). Sygnały przekazywane przez dendryty są wzmacniane lub osłabiane przez synapsy. Gdy suma ważonych sygnałów przekracza wartość progową następuje tzw. zapłon neuronu, który objawia się wygenerowaniem serii impulsów, przekazywanych przez akson do innych neuronów. Najcenniejszą cechą biologicznej sieci neuronowej jest zdolność do uczenia się, tzn. modyfikowania działania na podstawie kolejnych doświadczeń. Uczenie neuronów biologicznych polega między innymi na modyfikacji siły połączeń synaptycznych. W sztucznej sieci neuronowej odpowiada to modyfikacji wag.