Podręcznik
3. Perceptron wielowarstwowy
3.4. Funkcje kosztu
Do zastosowania algorytmów uczenia gradientowego (rozdział 2.2) wymagane jest wyznaczenie wartości funkcji kosztu \(J\) oraz jej pochodnych po parametrach sieci. W tym rozdziale zostaną omówione podstawowe funkcje kosztu.
W problemach regresji najczęściej stosujemy błąd średniokwadratowy (ang. MSE - Mean Squared Error) (wzór 14):
\[ \frac{1}{m} \sum_{j=1}^m (y_j - \hat{y}_j)^2 \]gdzie \( m \) jest liczbą przykładów, \( y_j \) prawidłową etykietą dla \( j \)-tego przykładu, a \( \hat{y}_j \) wyjściem sieci dla \( j \)-tego przykładu. Błąd średniokwadratowy polega na wyznaczeniu różnicy między prawidłową wartością a wyjściem sieci, podniesieniu do kwadratu i uśrednieniu dla wszystkich przykładów.
W problemach klasyfikacji binarnej (klasyfikacji dla dwóch klas) stosujemy binarną entropię krzyżową (ang. BCE - binary cross-entrophy) (wzór 15):
\[ -\frac{1}{m} \sum_{j=1}^m \left( y_j \log(\hat{y}_j) + (1 - y_j)\log(1-\hat{y}_j)\right) \]Funkcja ta na pierwszy rzut oka wydaje się trudna do zrozumienia. Spróbujmy zbudować sobie intuicje odnośnie jej działania. Dla pojedynczego przykładu (pomijamy sumowanie po \( m \)) rozważmy funkcję kosztu daną wzorem (wzór 16):
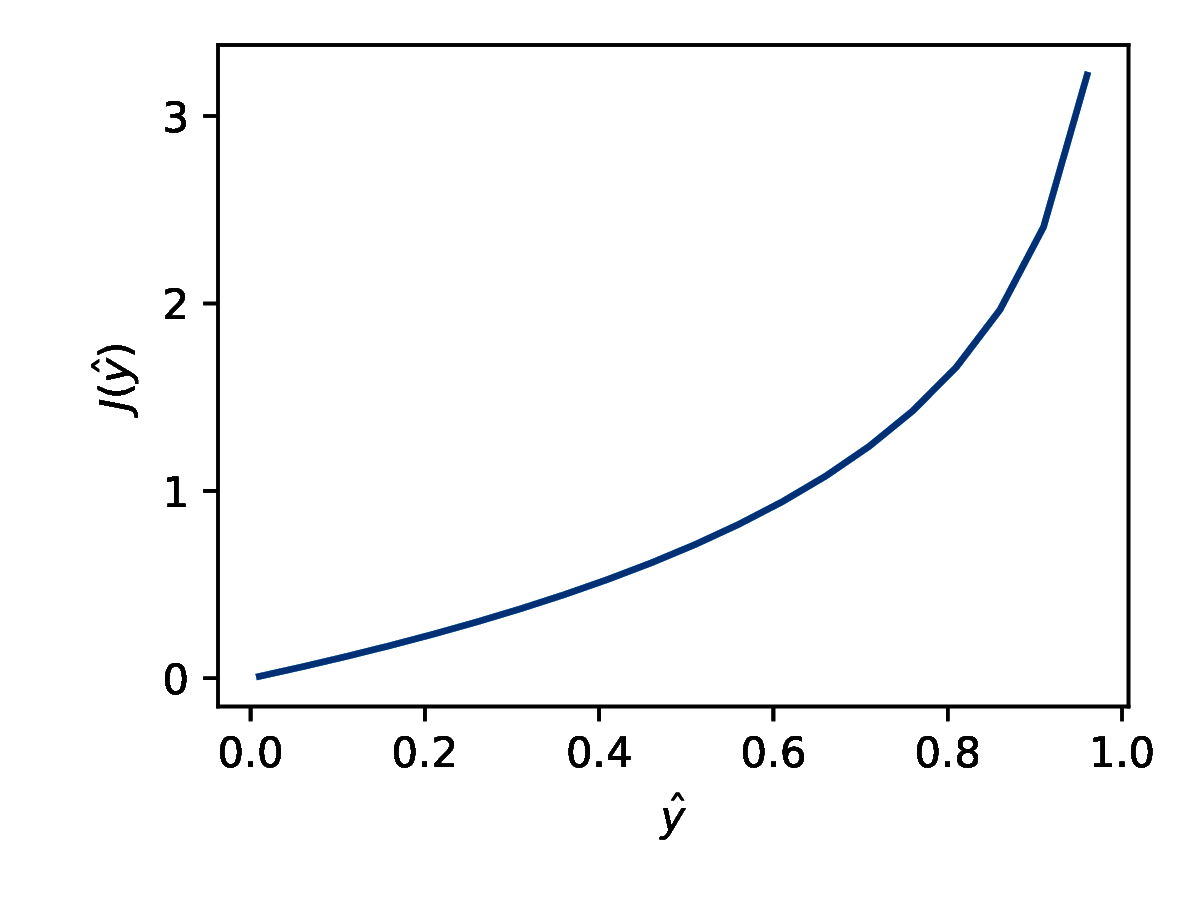
\[ \text{koszt}(\hat{y}^{(j)}, y^{(j)})= \begin{cases} -\log(\hat{y}^{(j)}) & \text{dla } y^{(j)}=1 \\ -\log(1 - \hat{y}^{(j)}) & \text{dla } y^{(j)}=0 \\ \end{cases} \]Dla problemów klasyfikacji binarnej w warstwie wyjściowej stosujemy sigmoidalną funkcję aktywacji i wyjście sieci ma wartości z zakresu (0, 1). Dla \( y = 0 \) rozważamy funkcję kosztu przedstawioną na wykresie 6a. Jeśli wyjście sieci \( \hat{y} \) ma wartość 0 to koszt jest zerowy. Im bliżej \( \hat{y} \) jest wartości 1 tym większa wartość funkcji kosztu, czyli dla predykcji nieprawidłowej klasy z dużą pewnością model dostaje silną negatywną informację zwrotną.
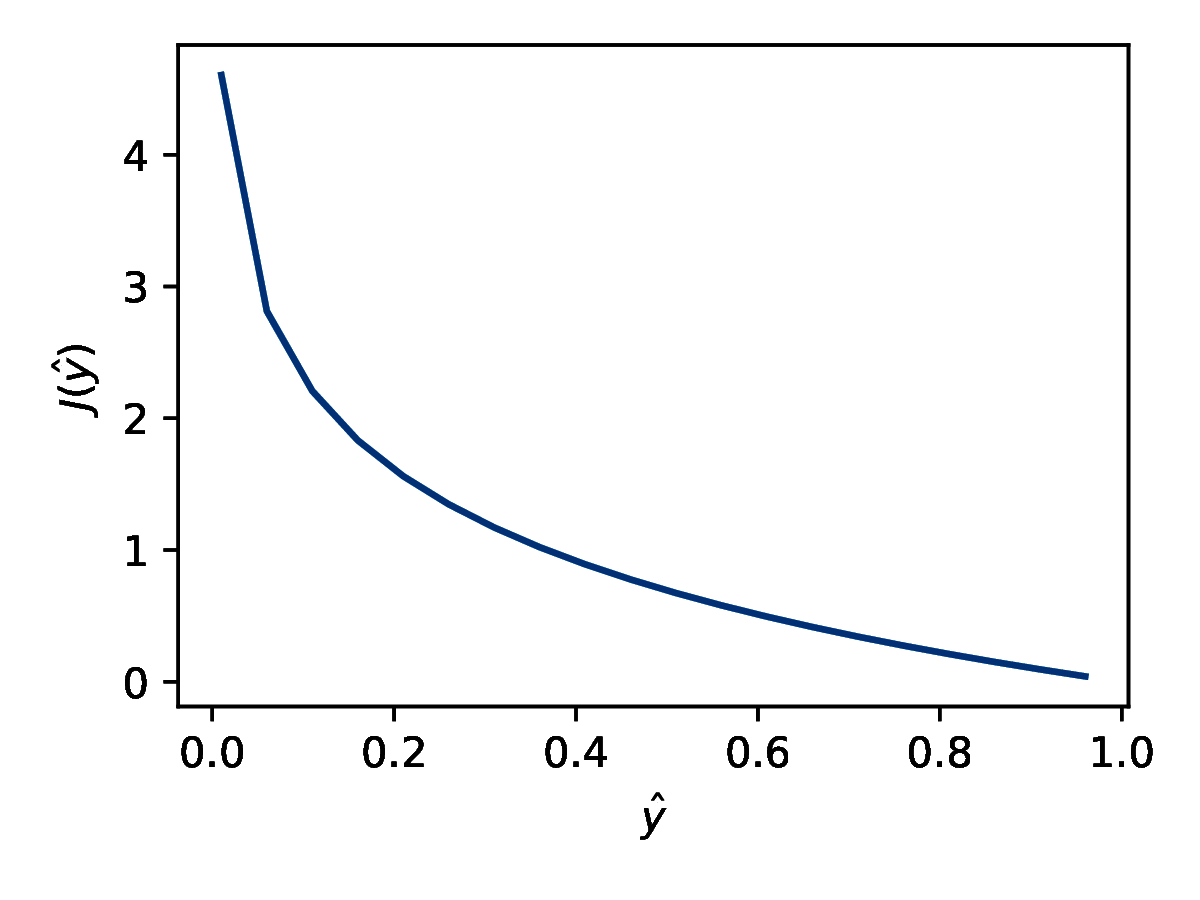
Odwrotnie dla \( y = 1 \) stosujemy funkcję kosztu przedstawioną na rysunku 6b. Jeśli \( \hat{y} = 1 \) to koszt jest zerowy. Im bliżej \( \hat{y} \) jest zera, tym większy koszt. Jeżeli przyjrzymy się uważnie wzorowi (15), dostrzeżemy, że jest to inna forma zapisu (16) (i dodatkowo uwzględnienie wielu przykładów).
Dla wielu klas stosujemy entropię krzyżową wieloklasową (ang. categorical cross-entrophy) (wzór 17):
\[ -\frac{1}{m} \sum_{j=0}^m \sum_{c=1}^M y_{jc}\log(\hat{y}_{jc}) \]gdzie \( M \) oznacza liczbę klas, a \( c \) jest indeksem klasy. Interpretacja jest taka sama jak dla binarnej entropii krzyżowej, ale tu uwzględniamy w wyliczeniu tylko wyjście sieci odpowiadające prawidłowej klasie.
