Podręcznik

W procesie uczenia sieci chcemy aktualizować wartości wag i wyrazów wolnych na podstawie danych uczących. Wagi sieci będziemy oznaczać $w_{kl}^{[i]}$, a wyrazy wolne $b_{k}^{[i]}$, gdzie $i$ jest indeksem warstwy, $k$ numerem neuronu w danej warstwie, a $l$ indeksem wagi neuronu.

Algorytm uczenia odbywa się w dwóch krokach:

1. W przód (ang. forward) - wyznaczenie wyjścia sieci i wartości funkcji kosztu J. Wyjście sieci wyznaczamy przeliczając aktywacje warstw - od pierwszej do ostatniej.

2. Wstecz (ang. backward) - wyznaczenie wszystkich pochodnych wag i wyrazów wolnych. Pochodne w warstwie [i] można wyznaczyć na podstawie pochodnych w warstwie [i+1]. Zatem obliczenia prowadzimy od ostatniej warstwy do pierwszej. Z tego wględu mówimy o algorytmie wstecznej propagacji błędów.

Obecnie dostępnych jest wiele narzędzi, które krok wstecz wykonują w sposób automatyczny, takich jak TensorFlow (https://www.tensorflow.org), PyTorch (https://pytorch.org/) lub JAX (https://github.com/google/jax). W tym module przedstawimy przykłady kodu z wykorzystaniem TensorFlow z interfejsem Keras.

Algorytm uczenia sieci przebiega w następujących krokach:

1. Przypisz wagom losowe wartości początkowe

2. Wyznacz wyjście sieci $\hat{y}$

3. Wyznacz wartość funkcji kosztu $J$

4. $dW = \frac{\partial J}{\partial W} \qquad db = \frac{\partial J}{\partial b}$ $W = W - \alpha dW$ $b = b - \alpha db$

5. dopóki nie warunek stopu idź do 2

Rysunek 7: Przykładowa sieć - zadaniem jest wyznaczenie pochodnych dla wag oznaczonych na niebiesko

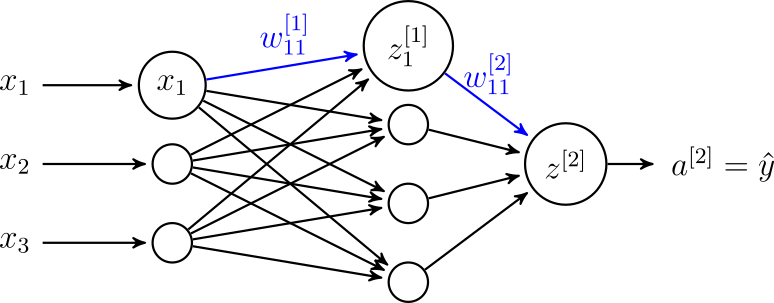
Rozważmy sieć przedstawioną na rysunku 7. Chcemy wyznaczyć $\frac{\partial J}{\partial w_{11}^{[1]}}$ (a po drodze $\frac{\partial J}{\partial w_{11}^{[2]}}$). Dla uproszczenia przyjmijmy, że wyznaczamy wyjście sieci $\hat{y}$ na podstawie jednego przykładu uczącego.

Przyjmijmy, że sieć realizuje zadanie klasyfikacji binarnej. Zatem odpowiednią funkcją kosztu jest binarna entropia krzyżowa (równanie 15) (wzór 18):

$J = -(y\log(\hat{y})+(1-y)\log(1-\hat{y}))$

Pochodna funkcji kosztu po wyjściu sieci $\frac{\partial J}{\partial \hat{y}}$ wynosi (wzór 19):

$\frac{\partial J}{\partial \hat{y}} = -\frac{y}{\hat{y}} + \frac{1 - y}{1 - \hat{y}}$

Wyjście sieci $\hat{y}$ odpowiada aktywacji neuronu ostatniej warstwy. Dla klasyfikacji binarnej stosujemy sigmoidalną funkcję aktywacji.

$\hat{y} = a^{[2]} = \frac{1}{1 + \exp(-z^{[2]})}$

gdzie $a^{[2]}$ jest aktywacją neuronu w warstwie drugiej, a $z^{[2]}$ wyjściem neuronu warstwy drugiej przed zastosowaniem funkcji aktywacji.

Pochodne wyznaczamy idąc wstecz, zatem w kolejnym kroku chcemy wyznaczyć $\frac{\partial J}{\partial z^{[2]}}$, korzystając przy tym ze wzoru na pochodną funkcji złożonej (wzór 20):

$\frac{\partial J}{\partial z^{[2]}} = \frac{dJ}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial z^{[2]}}$

Wartość $\frac{\partial J}{\partial \hat{y}}$ już wyliczyliśmy. Korzystając ze wzoru na pochodną funkcji sigmoidalnej (równanie 4) otrzymujemy (wzór 21):

$\frac{\partial \hat{y}}{\partial z^{[2]}} = \hat{y}(1 - \hat{y})$

Wstawiając (21) i (19) do (20) powyższe do wzoru otrzymujemy (wzór 22):

$\frac{\partial J}{\partial z^{[2]}} = \hat{y} - y$

Następnie wyznaczamy $\frac{\partial J}{\partial w_{11}^{[2]}}$ (wzór 23):

$\frac{\partial J}{\partial w_{11}^{[2]}} = \frac{dJ}{\partial z^{[2]}} \frac{\partial z^{[2]}}{\partial w_{11}^{[2]}}$

W tym celu potrzebujemy wyliczyć $\frac{\partial z^{[2]}}{\partial w_{11}^{[2]}}$. Pamiętamy (z równania 1), że (wzór 24):

$z^{[2]} = a_1^{[1]} w_{11}^{[2]} + \ldots + a_4^{[1]} w_{14}^{[2]} + b_1^{[2]}$

Zatem (wzory 25 i 26):

$\frac{\partial z^{[2]}}{\partial w_{11}^{[2]}} = a_1^{[1]}$ $\frac{\partial J}{\partial w_{11}^{[2]}} = \frac{dJ}{\partial z^{[2]}} a_1^{[1]}$

Wyznaczmy również pochodną dla wyrazu wolnego $b_1^{[2]}$ (wzór 27):

$\frac{\partial J}{\partial b_1^{[2]}} = \frac{dJ}{\partial z^{[2]}} \frac{\partial z^{[2]}}{\partial b_1^{[2]}} = \frac{dJ}{\partial z^{[2]}}$

Idąc dalej wgłąb wyliczamy $\frac{dJ}{\partial z_1^{[1]}}$ (wzór 28):

$\frac{dJ}{\partial z_1^{[1]}} = \frac{dJ}{\partial a^{[1]}} \varphi'(z_1^{[1]})$

gdzie $\varphi'(z_1^{[1]})$ jest pochodną funkcji aktywacji w warstwie pierwszej po $z_1^{[1]}$. W tej warstwie możemy zastosować różne funkcje aktywacji i konkretna postać wzoru będzie zależała od wybranej funkcji. Wykorzystując wcześniejsze wzory dostajemy (wzór 29):

$\frac{dJ}{\partial a^{[1]}} = \frac{dJ}{\partial z^{[2]}} w_{11}^{[2]}$

Zauważmy, że (wzór 30):

$z_1^{[1]} = w_{11}^{[1]} x_1 + \ldots + w_{13}^{[1]} x_3 + b_1^{[1]}$

Ostatecznie dostajemy (wzór 31):

$\frac{\partial J}{\partial w_{11}^{[1]}} = \frac{\partial J}{\partial z_1^{[1]}} \frac{\partial z_1^{[1]}}{\partial w_{11}^{[1]}} =\frac{dJ}{\partial z_1^{[1]}} x_1$

oraz (wzór 32)

$\frac{\partial J}{\partial b_{1}^{[1]}} = \frac{\partial J}{\partial z_1^{[1]}} \frac{\partial z_1^{[1]}}{\partial b_{1}^{[1]}} = \frac{dJ}{\partial z_1^{[1]}}$

Na podstawie wyznaczonych pochodnych możemy wykonać krok algorytmu gradientowego.

Mini-batche

Być może zauważyliście pewną niekonsekwencję pojawiającą się w dotychczasowych rozważaniach. W przykładzie obliczeniowym wyznaczaliśmy pochodne dla jednego przykładu, a w innych miejscach wspominany był cały zbiór uczący. Ogólnie algorytmy gradientowe stosujemy w trzech wariantach:

• Standardowa metoda spadku gradientu (ang. gradient descent) - w każdym kroku wyliczamy pochodne dla całego zbioru uczącego. Pozwala to na dokładne wyliczenie kierunku spadku funkcji kosztu dla całego zbioru, ale jest kosztowne obliczeniowo. W przypadku większych zbiorów danych (np. przetwarzanie obrazu) może być niewykonalne ze względu na niemożliwość jednoczesnego załadowania całego zbioru do pamięci RAM.

• Stochastyczna metoda spadku gradientu (ang. stochastic gradient descent) - w każdym kroku przetwarzamy tylko jeden przykład ze zbioru uczącego. Czas obliczeń w pojedynczym kroku się skraca, ale dostajemy jedynie oszacowanie gradientu dla całego zbioru. Taka metoda nie pozwala również na wykorzystanie zoptymalizowanych funkcji przetwarzających całe macierze.

• Przetwarzanie w mini-batchach (ang. batch gradient descent lub mini-batch gradient descent) - stanowi kompromis pomiędzy powyższymi metodami i jest najczęściej stosowane w praktyce. Dane uczące są przetwarzane w paczkach (ang. batch). Pozwala to na wydajne wykorzystanie możliwości sprzętu obliczeniowego.

Przejście przez cały zbiór danych uczących nazywamy epoką (ang. epoch).

Rozszerzenia metody gradientu prostego

Funkcje kosztu dla realnych problemów uczenia sieci neuronowych mają wiele lokalnych minimów i nie są wypukłe. Pewne wyzwanie stanowi również dobranie odpowiedniej wartości współczynnika uczenia α. Mogą występować takie problemy jak oscylacje, zanikające (płaska funkcja kosztu) lub wybuchające (stroma funkcja kosztu) gradienty.

Powstały modyfikacje metody gradientu prostego pozwalające na przyśpieszenie procesu uczenia. Do najbardziej popularnych algorytmów należą momentum [Qian, 1999], rmsprop [Hinton et al., ] i Adam [Kingma and Ba, 2014].

Literatura