Podręcznik: Metody regularyzacji

3. Perceptron wielowarstwowy

3.7. Metody regularyzacji

Metody regularyzacji służą do ograniczania zjawiska przeuczenia modelu.

Regularyzacja L2

Do najstarszych metod regularyzacji należą metody ograniczania wartości parametrów modeli. Przy dopasowywaniu funkcji wielomianowych zjawisko przeuczenia charakteryzuje się tym, że współczynniki dopasowanego wielomianu mają bardzo duże wartości bezwzględne (sytuacja taka wygląda jak na rysunku 3d). Podobne zjawisko możemy zaobserwować w sieciach neuronowych i dotyczy ono dużych wartości bezwzględnych wag oraz wyrazów wolnych. W celu zastosowania regularyzacji L2 [Hoerl and Kennard, 1970] modyfikujemy funkcję kosztu w następujący sposób:

$J(w) = \text{błąd jak dotychczas} + \lambda \sum_{i=1}^n w_i^2$

Duże wartości wag są karane proporcjonalnie do kwadratu ich wartości. Do członu odpowiadającego z regularyzację dodajemy wagę $\lambda$ (liczba dodatnia). Im większa wartość $\lambda$ tym silniejsza regularyzacja.

Gradient dla zmodyfikowanej funkcji kosztu jest następujący:

$\frac{\partial J}{\partial w_i} = \text{gradient jak dotychczas} + 2 \lambda w_i$

co oznacza, że wagi dodatnie są zmniejszane, a ujemne zwiększane. Siła zmniejszania/zwiększania jest proporcjonalna do wartości bezwzględnej wagi. Regularyzacja L2 silnie oddziałuje na wagi o dużych wartościach bezwzględnych.

Regularyzacja L1

Regularyzacja L1 [Tibshirani, 1996] działa bardzo podobnie do L2, ale kara nakładana jest na wartości bezwzględne wag. Otrzymujemy zmodyfikowaną funkcję kosztu:

$J(w) = \text{błąd jak dotychczas} + \lambda \sum_{i=1}^n |w_i|$

oraz gradient:

$\frac{\partial J}{\partial w_i} = \text{gradient jak dotychczas} + \lambda \operatorname{sign}(w_i)$

Należy zwrócić uwagę, że gradient zależy tylko od znaku danej wagi, co oznacza, że L1 oddziałuje tak samo silnie na małe i duże wagi. Interesującym efektem zastosowania L1 jest uzyskanie wartości części wag równych dokładnie 0.

Dropout

Dropout [Srivastava et al., 2014] (w przeciwieństwie do L1 i L2) jest metodą dedykowaną do sieci neuronowych. Rozważmy sieć przedstawioną na rysunku 8. Jest to sieć MLP, połączenia między warstwami zostały pominięte dla czytelności. Dropout polega na pominięciu w sposób losowy jakiejś części neuronów z danej warstwy w danym kroku algorytmu. Pominięte neurony zostały zaznaczone szarym kolorem i linią przerywaną na rysunku 8. Pominięcie oznacza, że wyjścia tych neuronów w danej iteracji są zerowane (wyjścia pozostałych neuronów warstwy są przeskalowywane), a algorytm gradientowy nie modyfikuje ich wag. W kolejnym kroku algorytmu neurony do pominięcia są losowane ponownie. Parametrem warstwy dropout jest prawdopodobieństwo pominięcia neuronów.

Rysunek 8: Dropout

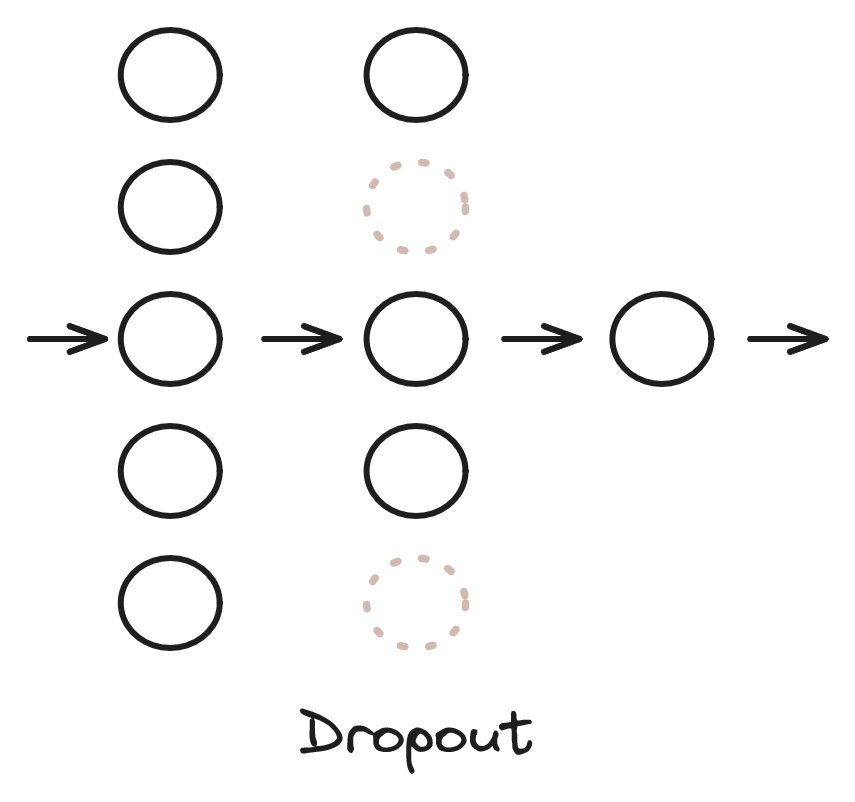
W nauczonym modelu wykorzystujemy już wszystkie neurony. Celem tej metody jest zabezpieczenie się przed nadmierną specjalizacją neuronów. Dropout można również interpretować jako jednoczesne uczenie wielu modeli (w każdej iteracji uczymy sieć o trochę innej strukturze).

Batch normalization

Jeżeli dane wejściowe modelu zmienią swój rozkład w stosunku do danych uczących, to działanie modelu zazwyczaj znacząco się pogorszy. Metoda batch normalization [Ioffe and Szegedy, 2015] próbuje normalizować dane wewnątrz paczek danych (batchy) w celu zapewnienia podobnego rozkładu danych wejściowych do kolejnych warstw.

Batch normalization działa w następujący sposób (wzory 33-36):

$\mu = \frac{1}{B} \sum_{b=1}^B x_b$

$\sigma^2 = \frac{1}{B} \sum_{b=1}^B (x_b - \mu)^2$

$\hat{x}_b = \frac{x_b - \mu}{\sqrt{\sigma^2 + \epsilon}}$

$y_b = \gamma \hat{x}_b + \beta$

gdzie $x_b$ jest wektorem danych wejściowych do warstwy batch normalization, $B$ rozmiarem batcha (liczbą przykładów), $\mu$ średnią liczoną w wymiarze batcha, a $\sigma^2$ odchyleniem standardowym. Następnie wyznaczane są znormalizowane wartości $\hat{x}_b$ ( $\epsilon$ - mała liczba dodatnia, służy zapewnieniu stabilności numerycznej - nie chcemy dzielić przez 0), a potem wartości $\hat{x}_b$ są przeskalowywane liniowo. Współczynniki $\gamma$ i $\beta$ należą do uczonych współczynników modelu. W ten sposób algorytm może dostosować dogodny zakres danych wejściowych dla kolejnej warstwy. $y_b$ jest wyjściem warstwy normalizacji.

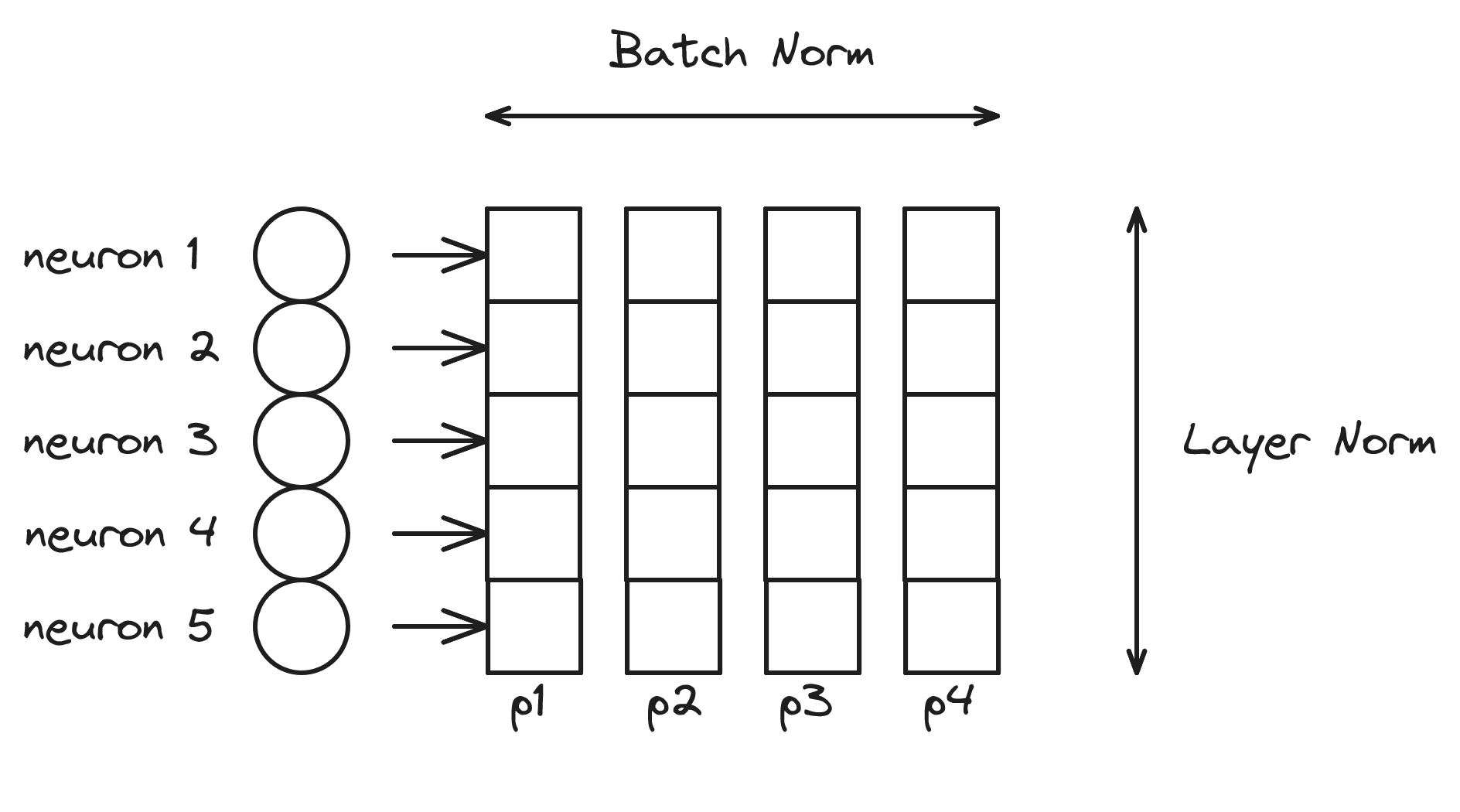
Ilustracja normalizacji batch - macierz danych z zaznaczonym kierunkiem normalizacji

Rysunek 9: Normalizacja względem batchy

Rozważmy warstwę sieci przedstawioną na rysunku 9. Warstwa ta ma 5 neuronów. Przetwarzamy batch o rozmiarze 4, złożony z przykładów $p1$ - $p4$ . Warstwa batch normalization normalizuje wartości w wymiarze batcha - średnia i odchylenie standardowe są liczone dla przykładów $p1$ - $p4$ . Przetwarzanie odbywa się dla każdej cechy (wyjść poszczególnych neuronów) niezależnie.

Spotykana jest również inna wersja normalizacji layer norm [Ba et al., 2016], która normalizuje wartości w wymiarze neuronów, czyli średnia i odchylenie standardowe wyznaczane są dla neuronów od 1 do 5. Zazwyczaj batch normalization spotykamy w przetwarzaniu obrazów (sieci konwolucyjne), a layer norm w przetwarzaniu tekstu (sieci rekurencyjne, transformery), ale nie ma przeszkód, aby metody te stosować do innych problemów i struktur sieci.

Literatura

[Srivastava et al., 2014]	Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: A simple way to prevent neural networks from overfitting. Journal of Machine Learning Research, 15(56):1929--1958. [ \| .html ]
[Ioffe and Szegedy, 2015]	Ioffe, S. and Szegedy, C. (2015). Batch normalization: Accelerating deep network training by reducing internal covariate shift. [ \| arXiv ]
[Ba et al., 2016]	Ba, J. L., Kiros, J. R., and Hinton, G. E. (2016). Layer normalization. [ \| arXiv ]
[Hoerl and Kennard, 1970]	Hoerl, A. E. and Kennard, R. W. (1970). Ridge regression: Biased estimation for nonorthogonal problems. Technometrics, 12(1):55--67.
[Tibshirani, 1996]	Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological), 58(1):267--288. [ \| http ]