Podręcznik

Sieci RBF (ang. radial basis function) to sieć, w której jako funkcje aktywacji stosujemy radialne funkcje bazowe [Broomhead and Lowe, 1988]. Radialna funkcja bazowa to funkcja, której wartość zależy tylko od odległości od określonego punktu.

(a) $\rho(r) = \exp(-\beta r^2)$

(b) $\rho(r) = \frac{1}{1 + \beta r^2}$

Rysunek 25: Przykłady radialnych funkcji bazowych

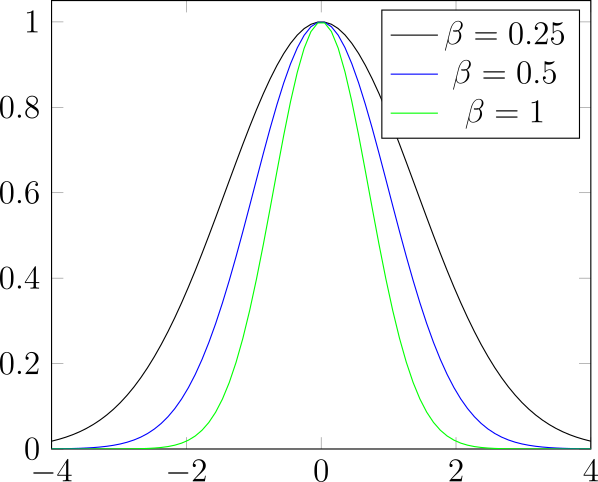
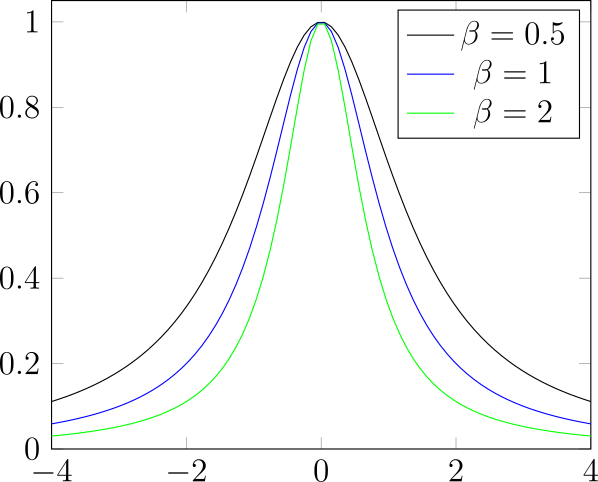
Przykłady radialnych funkcji bazowych zostały przedstawione na rysunku  25. Neurony o radialnych funkcjach aktywacji możemy interpretować jako sprawdzające jak blisko dane wejściowe są określonego punktu.

Sieci RBF możemy wykorzystywać w zadaniach regresji (aproksymacji funkcji) oraz klasyfikacji.

(a) Uczenie dyskryminacyjne

(b) Uczenie generacyjne

Rysunek 26: Uczenie generacyjne a dyskryminacyjne

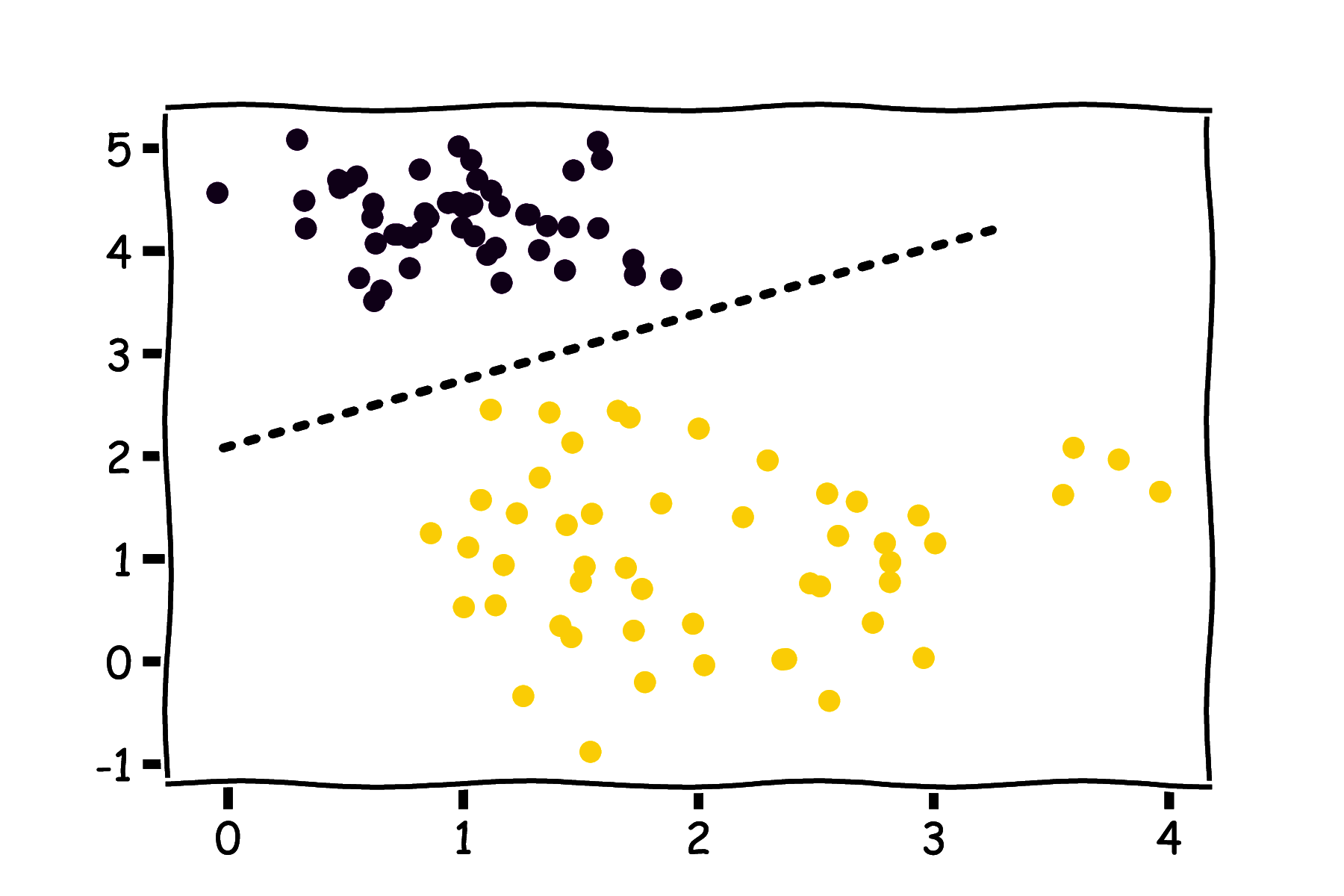
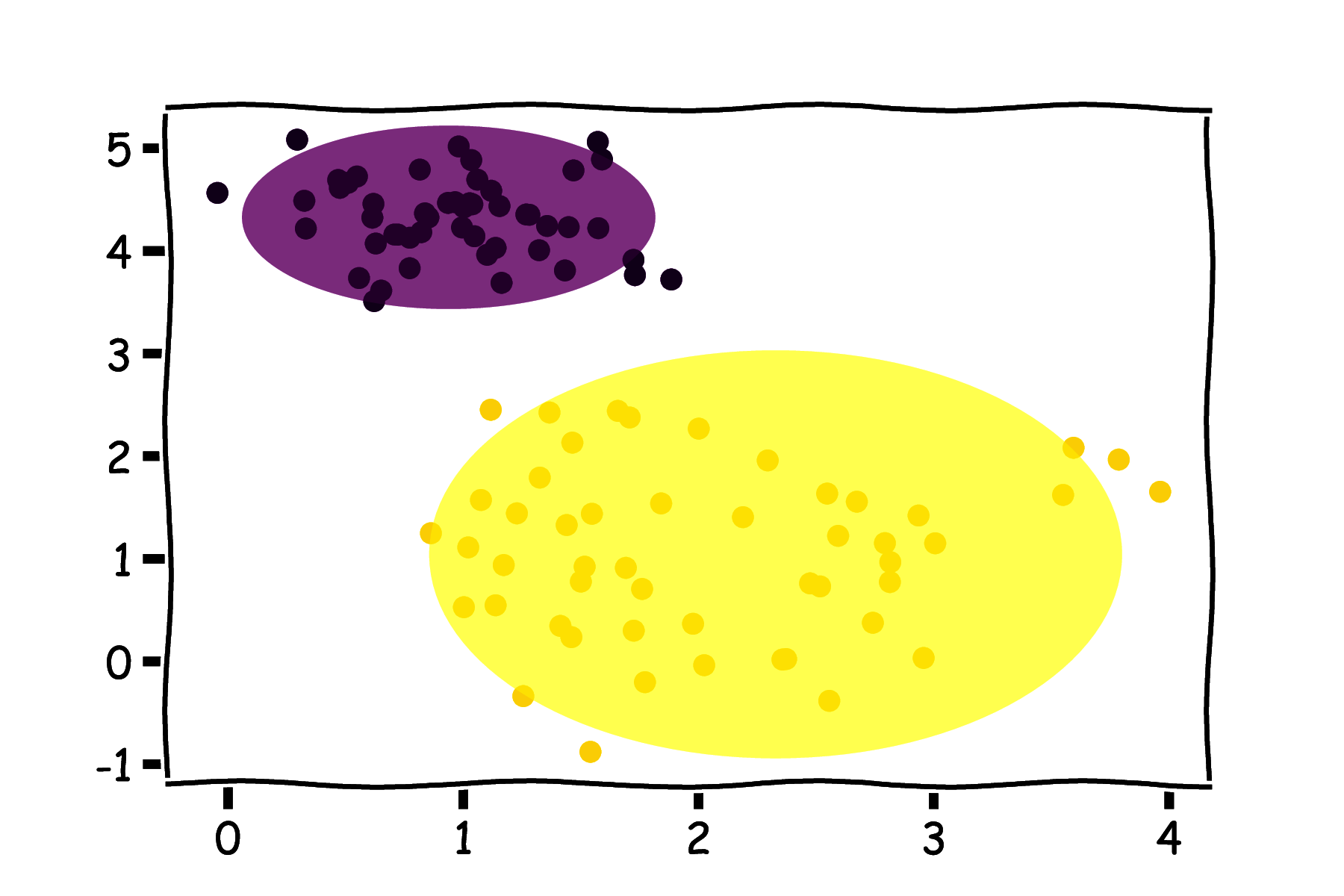
Możemy zauważyć, że w neuronach RBF mamy do czynienia z pewną zmianą paradygmatu w stosunku do perceptronu. Perceptron realizuje liniowy podział przestrzeni danych wejściowych (rysunek 26a), natomiast neuron RBF wybiera pewien podzbiór przestrzeni danych wejściowych ograniczony odległością do konkretnego punktu (rysunek 26b).

Rysunek 27: Sieć RBF

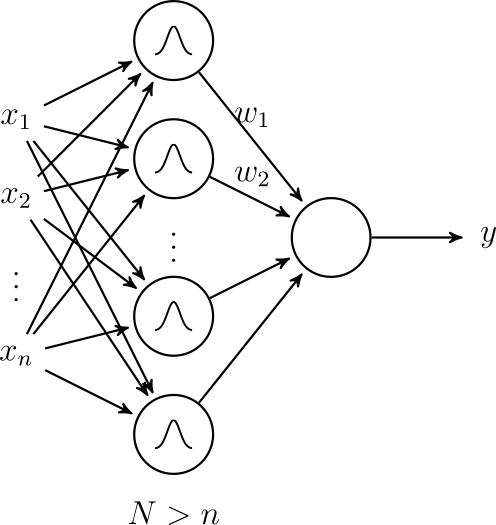
Struktura całej sieci RBF została przedstawiona na rysunku 27. Zawiera ona tylko jedną warstwę ukrytą z neuronami o radialnych aktywacjach. Odpowiada to przekształceniu przestrzeni zmiennych wejściowych w inną przestrzeń (o większej liczbie wymiarów), z nadzieją, że w nowej przestrzeni uda się zrealizować dopasowanie liniowe. Jest to popularne podejście w uczeniu maszynowym (tzw. kernel trick).

Warstwa wyjściowa sieci realizuje dopasowanie liniowe (wzór 37):

gdzie $c_i$ to punkt centralny dla neuronu $i$.

Uczenie sieci RBF składa się z dwóch kroków. W pierwszym, w sposób nienadzorowany, dobierane są środki c_i. Mogą być one wybrane losowo spośród punktów z danych uczących lub z wykorzystaniem algorytmów grupowania (np. k-średnich). Następnie wagi w_i są uczone w sposób nadzorowany. Można tu wykorzystać dobrze już nam znane algorytmy gradientowe lub inne metody dopasowywania współczynników funkcji liniowej.

Sieci RBF zostały zaproponowane przed rozwojem uczenia głębokiego i najczęściej nie znajdziemy ich wprost w pakietach do uczenia głębokiego jak Keras. Jednak własna implementacja nie stanowi większego problemu ze względu na prostotę rozwiązania.

Literatura