Podręcznik
Wstęp do logiki rozmytej
1. Wprowadzenie do teorii zbiorów rozmytych
1.1. Co to są zbiory rozmyte?
Jednym z fundamentów matematyki jest bez wątpienia teoria mnogości, a jej podstawowym elementem jest pojęcie zbioru. Nie wdając się w zbyt formalne rozważania, przeliczalny zbiór Z możemy określić w postaci enumeratywnej np. jako podzbiór złożony z n elementów \( x_i\in X \).
| \( Z = \left\{x_1, x_2, x_3, x_4, ... x_n\right\} \) | (1) |
|---|
Jeśli \( X=\left\{N\right\} \), gdzie N jest zbiorem liczb naturalnych, to np.: zbiór liczb naturalnych wyrażających: całkowite oceny postępów w nauce można w notacji (1) zapisać w postaci:
| \( Z = \left\{1, 2, 3, 4, 5, 6\right\} \) | (2) |
|---|
Z oczywistych powodów powyższy zapis jest użyteczny tylko wówczas gdy liczba \( n \) elementów zbioru Z jest niewielka. Ten sam zbiór Z można określić również w postaci:
| \( Z = \left\{x\in X: W(x)\right\} \) | (3) |
|---|
gdzie: \( W(x) \) jest pewną właściwością elementów zbioru \( Z \). Właściwość \( W(x) \) pozwala na przyporządkowanie do zbioru \( Z \) tych elementów zbioru \( X=\left\{x\right\} \), które spełniają warunek \( W(x) \).
Jeśli \( X=\left\{N\right\} \) jest zbiorem liczb naturalnych, to zbiór liczb naturalnych wyrażających np. zbiór całkowitych i pozytywnych ocen postępów w szkole średniej można zapisać w postaci:
| \( Z = \left\{x\in N: 2 \leqslant x \leqslant 6\right\} \) | (4) |
|---|
Jeśli \( X=\left\{R\right\} \) jest zbiorem liczb rzeczywistych, to zbiór dodatnich liczb rzeczywistych można zapisać w postaci (4) lub w postaci:
| \( Z = \left\{x\in R: x > 0\right\} \) | (5) |
|---|
Innym sposobem notacji zbioru \( Z \) jest zdefiniowanie jego funkcji charakterystycznej. Funkcją charakterystyczną zbioru \( Z \) jest taka funkcja \( \phi(x) \), która każdemu elementowi zbioru \( Z \) przypisuje wartość 1 lub 0 zależnie od tego czy element ten należy (\( \phi(x)=1 \)), czy też nie należy (\( \phi(x)=0 \)) do tego zbioru.
| \( \phi(x) : X \rightarrow\ \left\{0,1\right\} \) | (6) |
|---|
taka, że:
| \( \phi(x) = \left\{ \begin{array}{c} 0\;\ dla\;\ x\notin Z\\ 1 \;\ dla\;\ x\in Z\\ \end{array}\right. \) | (7) |
|---|
Stąd równoważną formą notacji zbioru \( Z \) z funkcją charakterystyczną jest zbiór par:
| \( Z = \left\{\left(\phi(x),x\right)\right\} \) | (8) |
|---|
Jeśli \( X=\left\{N\right\} \), gdzie \( N \) jest zbiorem liczb naturalnych, to zbiór liczb naturalnych wyrażających całkowite pozytywne oceny postępów w nauce w szkole średniej można zapisać w postaci (4) lub postaci par:
| \( Z = \left\{(0,0), (0,1), (1,2), (1,3), (1,4), (1,5), (1,6) (0,7),\, ...\,\right\} \) | (9) |
|---|
Jak więc widzimy dwuwartościowa funkcja charakterystyczna pozwala na wskazanie, które z elementów zbioru \( X \) należą, a które nie należą do zbioru \( Z \).
Zważmy dalej, że definicje (1), (3) i (7) są definicjami ściśle określonymi. W praktyce używa się jednak pewnych sformułowań i pojęć określonych w sposób nieścisły np: "wysokie ciśnienie", "średni wzrost", "niska inflacja", "niewielka odchyłka regulacji" itp. I tu pojawia się pytanie, czy tak nieprecyzyjne sformułowania można w jakikolwiek sposób wyrazić w sposób sformalizowany? Jeśli założymy, że tak to jak łatwo zauważyć natychmiast pojawiają się następne trudności, bowiem pod pojęciem "duża masa" będziemy rozumieli prawdopodobnie zupełnie coś innego w odniesieniu do przysłowiowej myszy i słonia. W naturalny sposób pojęcie "duża masa" wyraża w jakiś sposób zrelatywizowaną informację odwołując się do relacji pomiędzy pewną właściwością obiektu (masą), a pomiędzy pewną właściwością uznaną za normatywną (wzorcową lub odniesienia), przy czym zarówno jedna jak i druga nie muszą być zawsze zdefiniowane precyzyjnie. Ocena zatem co jest "duże", a co "małe" jest oceną z jednej strony zrelatywizowaną, z drugiej zaś oceną subiektywną w tym sensie, że zależy nie tylko od przyjętej normy relacji, ale również pewnej formy wnioskowania przyjętego w trakcie dokonywania oceny.
Np.: czy "wysoki wzrost mężczyzny" to: 180cm, czy 190cm, a może 200cm. Widać wyraźnie, że zaliczenie mężczyzny o wzroście 180cm do grupy mężczyzn o wysokim wzroście niekoniecznie musi być jednoznaczne przez wszystkich oceniających, a jeśli już, to jest uwarunkowane miejscem i czasem oceny. Oczywiście można tutaj wprowadzić ścisłą granicę uznając, że każdy z mężczyzn o wzroście powyżej 180cm jest wysokim mężczyzną, a każdy, którego wzrost jest poniżej 180cm jest już mężczyzną o niskim wzroście. Cóż wtedy powiedzą mężczyźni o wzroście 179cm, którzy będą mogli poczuć się urażeni.
Na Olimpiadzie Zimowej w 2002 r. w Salt Lake City w konkursie drużynowym skoków narciarskich złoty medal zdobyła drużyna niemiecka. Zwycięstwo osiągnęła zdobywając 740,1 punktów to znaczy zaledwie o 0,1 punktu więcej niż druga w kolejności drużyna fińska. W przeliczeniu na metry daje to wynik różniący się o 5 cm. Pomiary w konkursach skoku wykonywane są z rozdzielczością 0,5m. Czy drużyna fińska może poczuć się rozczarowana takim rozstrzygnięciem jury? Wydaje się że tak, ponieważ właściwsze byłoby rozstrzygnięcie ex aequo. Pojawia się w związku z tym pytanie, czy w związku z tym dyskretna ocena jest uzasadniona we wszystkich przypadkach?
W 1965 roku Zadeh [1] wprowadził pojęcie zbioru rozmytego. Analogicznie do (8) zbiór rozmyty \( A \) został określony w pewnej przestrzeni \( X \) zwanej dalej przestrzenią rozważań. Zbiór rozmyty \( A \) można przedstawić w postaci zbioru par:
| \( A = \left\{\left(\mu_A(x),x\right)\right\} \) | (10) |
|---|
gdzie:
| \( A = \mu_A(x):X\rightarrow \left[0,1\right] \) | (11) |
|---|
jest funkcją przynależności, która każdemu elementowi przestrzeni \( X \) przyporządkowuje stopień przynależności \( \mu_A(x) \) do danego zbioru rozmytego \( A \) począwszy od całkowitej nieprzynależności (\( \mu_A(x)=0 \)), przez przynależność częściową (\( 0<\mu_A(x)<1 \)), aż do przynależności całkowitej (\( \mu_A(x)=1 \)). W odróżnieniu od funkcji charakterystycznej, w której mamy do czynienia albo z "całkowitą nieprzynależnością" albo z "całkowitą przynależnością", występuje tutaj przypadek przynależności częściowej. Dla ilustracji załóżmy, że funkcja przynależności zbioru rozmytego \( WM \) ("wysoki mężczyzna") ma postać jak na rysunku poniżej.
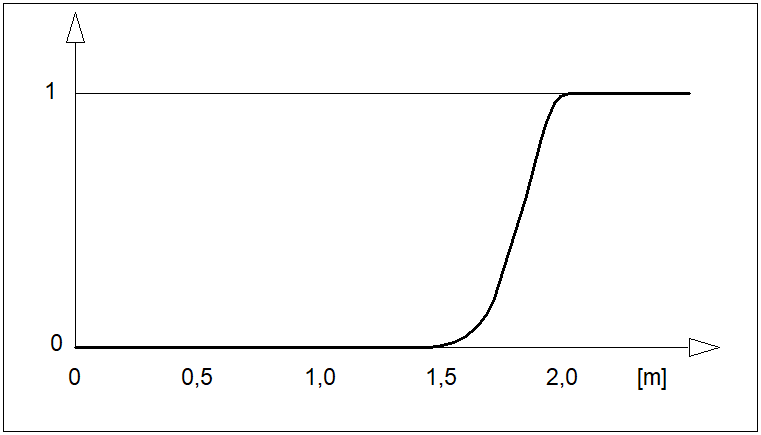
Przebieg funkcji przynależności z rysunku powyżej można interpretować następująco: mężczyznę o wzroście poniżej 150 cm na pewno nie można zaliczyć do grupy mężczyzn wysokich. Do grupy wysokich, z całą pewnością zaliczymy tych mężczyzn, których wzrost przekracza 200 cm. Mężczyzna o wzroście 180 cm jest w znacznym stopniu mężczyzną wysokim, a stopień przynależności tego mężczyzny do grupy wysokich mężczyzn może być odczytany bezpośrednio z przebiegu funkcji przynależności. Zwróćmy dalej uwagę, że funkcja przynależności ma w tym przypadku charakter czysto subiektywny. Jej przebieg zależy nie tylko od miejsca, czasu i osoby definiującej tę funkcję. Zwróćmy także uwagę, że dyskretna funkcja przynależności jest przypadkiem zdegenerowanymi i szczególnym funkcji ciągłej, a zatem definicję zbioru o postaci (10) należy uznać za bardziej ogólną od definicji (8).
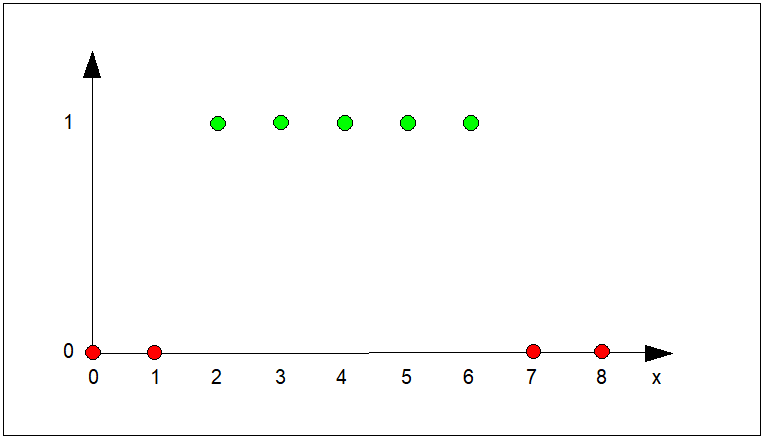
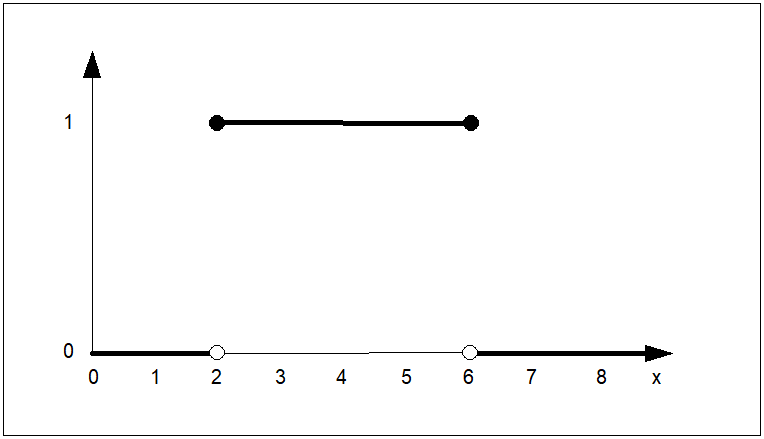
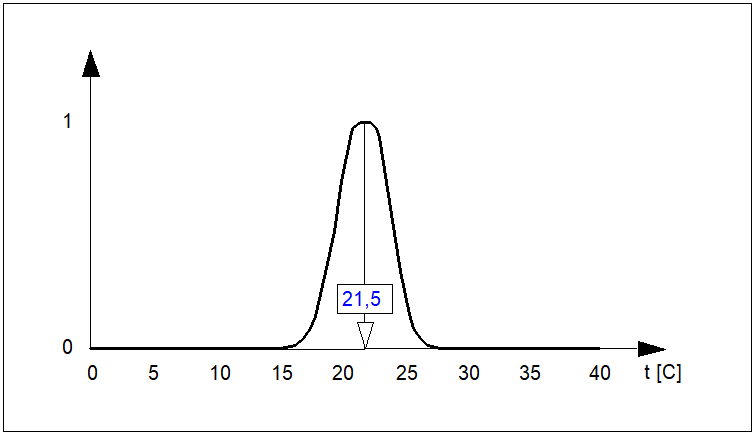
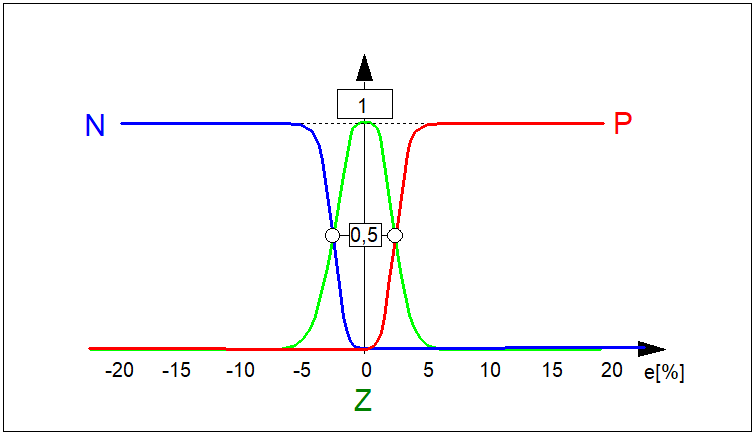
Rys. 5. Przykład przebiegu ciągłych funkcji przynależności:
\( \mu_N(e) \) zbioru rozmytego \( N \) ("ujemna odchyłka regulacji"),
\( \mu_Z(e) \) zbioru rozmytego \( Z \) ("zerowa odchyłka regulacji"),
\( \mu_P(e) \) zbioru rozmytego \( N \) ("dodatnia odchyłka regulacji").
Przebieg tych funkcji jest istotny w zastosowaniach logiki rozmytej w automatyzacji procesów technicznych.
Z podanych przykładów wynika, że funkcja przynależności może mieć postać zarówno funkcji ciągłej, nieciągłej lub przedziałami ciągłej.
