Podręcznik
Wstęp do logiki rozmytej
2. Elementy teorii zbiorów rozmytych
2.1. Zbiór rozmyty
Zbiór rozmyty, jak to już wspomnieliśmy wcześniej, służy do formalnego zdefiniowania pojęć nieostrych, nieprecyzyjnych czy wieloznacznych np. "mała odchyłka regulacji", "szeroka strefa histerezy", "duże przeregulowanie", "stan bliski granicy stabilności".
Rzecz jasna są to pojęcia relatywne. Weźmy dla przykładu pojęcie "duża liczba". Inną liczbę będziemy uważali za dużą, jeśli ograniczymy się do przedziału \( [0,10] \), a inną w przypadku gdy ograniczymy się np.: do przedziału \( [0,100] \). W pierwszym przypadku liczbę 9 będziemy traktowali jako dużą, w drugim przypadku tę samą liczbę będziemy traktowali jako małą. Tak więc pojęcie zbioru rozmytego wymaga określenia przestrzeni rozważań, będącej nierozmytym zbiorem elementów, w obrębie której się poruszamy. Może to być przedział liczbowy np.: \( [1..5] \), zbiór imion np.: \( \left\{Jan, Maciej, Maria\right\} \), zbiór cech np.: \( \left\{niski, średni, wysoki\right\} \), itp. Przestrzeń rozważań będziemy oznaczali dużymi literami łacińskimi np. \( X=\left\{x\right\} \) lub w przypadku skończeniewymiarowym \( X=\left\{x_1, x_2, x_3, x_4, ... x_n\right\} \).
Zbiorem rozmytym \( F \) w pewnej przestrzeni rozważań \( X=\left\{x\right\} \), co zapisujemy jako \( F\subseteq X \) nazywamy zbiór par:
| \( F=\left\{\left(\mu_F(x),x\right)\right\};\;\forall x\in X \) | (12) |
|---|
gdzie: \( \mu_F(x): X\to[0, 1] \) jest funkcją przynależności zbioru rozmytego \( F \), która każdemu elementowi \( x\in X \) przypisuje jego stopień przynależności do zbioru rozmytego \( F \); \( mu_F(x)\in [0, 1] \).
Porównując definicję (12) z (7) i (8) można interpretować funkcję przynależności jako uogólnioną funkcję charakterystyczną.
Dla uproszczenia dalszych rozważań parę \( \left\{\mu_F(x), x\right\} \) oznaczać będziemy \( \mu_F(x)/x \), a zbiór rozmyty o nieskończenie wielkiej liczbie elementów symbolem \( X=\left\{x\right\} \):
| \( \sum_{x\in X} \mu_F(x)/x \) | (13) |
|---|
Dla przestrzeni o skończonej liczbie elementów \( X = \left\{x_1, x_2, x_3, x_4, ... x_n\right\} \) :
| \( \sum_{i=1}^n \mu_F(x_i)/x_i= \mu_F(x_1)/x_{1}+\mu_F(x_2)/x_{2}+\dots+ \mu_F(x_n)/x_{n} \) | (14) |
|---|
gdzie symbole: \( \sum \) i \( + \) są symbolami sumy mnogościowej. Zapisy (13) i (14) oznaczają, że zbiór rozmyty jest sumą mnogościową elementów \( x_i \). W zapisie zbioru rozmytego pomijane są te pary, dla których \( mu_F(x)=0 \).
Pojęcie duża liczba.
Załóżmy przestrzeń rozważań \( X \) o skończonej liczbie elementów \( X=\left\{0, 1, 2, ..., 10\right\} \). Niech "duża liczba" określona w tej przestrzeni będzie miała postać następującego zbioru rozmytego o nazwie \( DL \):
| \( DL = 0,1/5 + 0,3/6 + 0,5/7 + 0,7/8 + 0,9/9 + 1,0/10 \) | (15) |
|---|
Interpretację graficzną tego zbioru przedstawia rysunek poniżej.
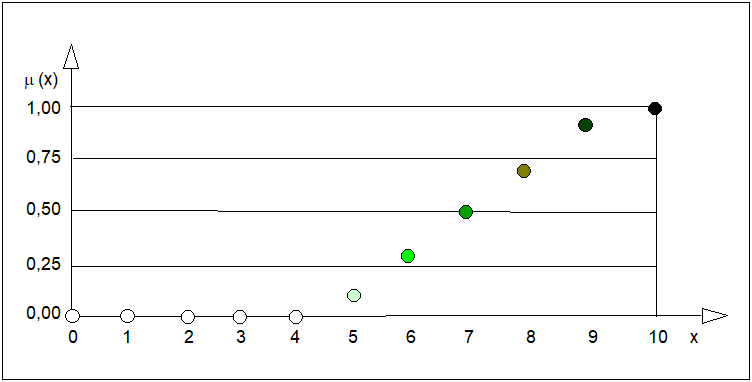
Pojęcie "duża liczba" można również przedstawić w przestrzeni o nieskończenie wielkiej liczbie elementów \( X =[0, 10] \). Wówczas funkcję \( mu_{DL}(x) \) wygodniej jest przedstawić w postaci analitycznej lub graficznej jak np. na rysunku poniżej.
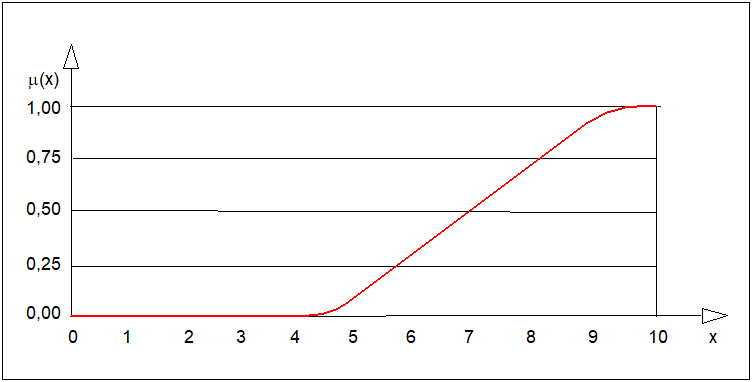
Na gruncie klasycznej teorii zbiorów nierozmytych liczba \( x \) w powyższym przykładzie mogłaby: albo należeć albo nie należeć do zbioru "duża liczba". To dwuwartościowe rozstrzygnięcie nie jest wygodne w przypadku, gdy o liczbie trudno powiedzieć czy jest liczbą dużą czy też nie (np.: liczba 5 w przykładzie). W przypadku zbiorów rozmytych o liczbie 5 można powiedzieć, że w stopniu równym 0,1 jest liczbą dużą. Funkcja przynależności pozwala zatem na rozmytą kwantyfikację elementów zbioru rozmytego. Z tego powodu dość często, choć nieprecyzyjnie, będziemy utożsamiać pojęcie zbioru rozmytego z jego funkcją przynależności.
Warto na chwilę zatrzymać się nad zbiorem wartości funkcji przynależności \( mu_{F}(x) \). Zbiór tych wartości należy do przedziału liczbowego \( [0, 1] \). Przedział ten przyjęto głównie dla prostoty. Tę samą rolę, tzn. wprowadzenie pewnego uporządkowania mógłby równie dobrze spełnić dowolny zbiór całkowicie uporządkowany.
Zbiór rozmyty \( F\subseteq X \) jest pusty, co zapisujemy \( F = 0 \) wtedy i tylko wtedy gdy \( mu_F(x) = 0 \) dla każdego \( x\in X \).
| \( F = \textbf{0}\Leftrightarrow\ \mu_F(x)=0 \; ;\;\forall x\in X \) | (16) |
|---|
Zbiór rozmyty \( F\subseteq X \) azwiemy zbiorem jednostkowym, co zapisujemy \( F = 1 \) wtedy i tylko wtedy gdy \( mu_F(x) = 1 \) dla każdego \( x\in X \).
| \( F = \textbf{1}\Leftrightarrow\ \mu_F(x)=1 \; ;\;\forall x\in X \) | (17) |
|---|
Z definicji (17) wynika, że każdy zbiór nierozmyty może być traktowany jako szczególny przypadek zbioru rozmytego z jednostkową funkcją przynależności. Oznacza to dalej, że działania na zbiorach rozmytych mają charakter uogólniający i mogą być, drogą podstawień typu: \( \mu_F(x) = 1 \) sprowadzone do działań na zbiorach nierozmytych.
Zbiór wszystkich elementów zbioru rozmytego, którym przyporządkowano niezerową wartość funkcji przynależności nazywać będziemy dalej nośnikiem lub suportem zbioru rozmytego.
Nośnikiem (suportem) zbioru rozmytego \( F \) jest zbiór nierozmyty elementów \( x \in X \), spełniających warunek:
| \( support(F)=\left\{x\in X : \mu_F(x)>0\right\} \) | (18) |
|---|
Jak łatwo zauważyć, suport zbioru pustego jest pusty, a suport zbioru jedynkowego zawiera wszystkie elementy zbioru \( X \).
Wartość funkcji przynależności zgodnie z definicją przyjmuje wartości z przedziału \( [0, 1] \). Nie oznacza to jednak, że wartość maksimum każdej funkcji przynależności jest zawsze równe \( 1 \). W teorii zbiorów rozmytych wprowadzono pojęcie wysokości zbioru rozmytego. Wysokość zbioru rozmytego jest liczbowo równa wartości maksimum globalnego funkcji przynależności.
Wysokością zbioru rozmytego \( F\subseteq X \) jest wartość maksymalna funkcji przynależności tego zbioru dla każdego \( x \in X \).
| \( h(F)=\bigcup_{x\in X}\mu_F(x) \; ;\;\forall x\in X \) | (19) |
|---|
Oczywiście jeśli \( \mu_F(x) \in [0,1] \Leftarrow h(F) \in [0,1] \).
Jak łatwo zauważyć, wysokość zbioru pustego \( F = 0 \) jest równa 0, zaś wysokość zbioru jednostkowego \( F = 1 \) jest równa 1.
Wysokość zbioru.
Załóżmy przestrzeń rozważań \( X \) o skończonej liczbie elementów \( X= \left\{0, 1, 2, ..., 10\right\} \). Określmy zbiór rozmyty \( F \) w tej przestrzeni w postaci:
| \( F= 0,1/1 + 0,3/3 + 0,5/5 + 0,4/7 + 0,2/9 \) | (20) |
|---|
Wysokością tego zbioru jest wartość \( h(F)=0,5 \).
Wysokość zbioru.
Załóżmy ciągłą przestrzeń rozważań \( X=[0, 100] \). Określmy zbiór rozmyty \( F \) w tej przestrzeni, którego funkcja przynależności opisuje kształt funkcji przynależności zbioru rozmytego "komfortowa temperatura" przedstawionego na rys. 4:
| \( \mu_F(x)=e^{-\left(\frac{x-21,5}{1,5}\right)^2} \) | (21) |
|---|
Wysokością tego zbioru jest wartość \( h(F)=1,0 \).
