Podręcznik: Operacje na zbiorach rozmytych

2. Elementy teorii zbiorów rozmytych

2.2. Operacje na zbiorach rozmytych

Zbiorem subnormalnym lub podnormalnym będziemy określali każdy niepusty zbiór rozmyty $F\subseteq X$ , którego wysokość $h(F)$ jest mniejsza od 1.

Niepusty subnormalny zbiór rozmyty może być przekształcony do postaci zbioru znormalizowanego przez zastosowanie odpowiedniego przekształcenia (operacji normalizacji).

Unormowaniem lub normalizacją subnormalnego zbioru rozmytego $F\subseteq X$ nazywać będziemy operację przekształcenia go w zbiór rozmyty $F^N\subseteq X$ o wysokości $h(FN)=1$ . Funkcję przynależności tego zbioru wyznaczymy przez operację skalowania zgodnie z (21):

$\mu_{F^N(x)}=\frac{\mu_F(x)}{h(F)} \; ;\;\forall x\in X \; ;\;h(F)\ne 0$	(22)

Normalizacja zbioru rozmytego.

Załóżmy przestrzeń rozważań $X$ o skończonej liczbie elementów $X= \left\{0, 1, 2, ..., 10\right\}$ . Określmy zbiór rozmyty $F$ w tej przestrzeni jak w przykładzie 6:

$F = 0,1/1 + 0,3/3 + 0,5/5 + 0,4/7 + 0,2/9$	(23)

Wysokością tego zbioru jest wartość $h(F)=0,5$ . Zbiór $F$ jest więc zbiorem subnormalnym. Unormowany zbiór rozmyty $F^N$ będzie miał następującą postać:

$F^N = 0,2/1 + 0,6/3 + 1,0/5 + 0,8/7 + 0,4/9$	(24)

Normalizacja zbioru jest w istocie operacją mnożenia zbioru rozmytego przez skalar $\beta$ o wartości:

$\beta= h(F) ^{-1}\; ;\;\forall x\in X$	(25)

Iloczyn zbioru rozmytego $F\subseteq X$ i nieujemnej liczby rzeczywistej $\beta$ , co oznaczać będziemy jako $\beta F$ , definiujemy w postaci:

$\mu_{F\beta}(x)= \beta \cdot \mu_F(x)$	(26)

gdzie: $\forall x\in X$ ; $\beta \in \left\{0, R^{+}\right\}$ ; $\mu_{F}(x) \in [0, 1]$ .

Z Def. 8 wynika, że: $0\leqslant \mu_{\beta F}(x) \leqslant 1 \forall x\in X$ oraz właściwość przemienności względem operacji mnożenia:

$\beta \cdot\mu_F(x)= \mu_F(x)\cdot\beta$	(27)

Jeśli $\beta \ne 1$ i $h(F) = 1$ to operacja zdefiniowana powyżej może być określana mianem denormalizacji zbioru normalnego.

Iloczyn zbioru rozmytego i liczby rzeczywistej

Niech $X \in [0, 10]$ ; $\beta =0,2$ ; zaś:

$F = 0,10/1 + 0,20/2 + 0,30/3 + 0,40/4 + 0,30/5 + 0,20/6$	(28)

stąd:

$\beta \cdot F = 0,02/1 + 0,04/2 + 0,06/3 + 0,08/4 + 0,06/5 + 0,04/6$	(29)

W analogiczny sposób do (27) zdefiniujemy teraz iloczyn arytmetyczny dwóch zbiorów rozmytych.

Iloczynem dwóch zbiorów rozmytych $F,G \subseteq X$ , jest taki zbiór rozmyty $FG$ , którego funkcja przynależności jest iloczynem funkcji przynależności obu tych zbiorów:

$\mu_{FG}(x) = \mu_{F}(x)\times \mu_{G}(x)\; ;\;\forall x\in X$	(30)

gdzie: $\forall x\in X$ ; $\beta \in \left\{0, R^{+}\right\}$ ; $\mu_{F}(x) \in [0, 1]$ .

Z Def. 9 wynika, że dla normalnych zbiorów $F,G \subseteq X$ i $\forall x\in X$ zachodzi:

$0\leqslant \mu_{FG}(x)\leqslant 1$	(31)

oraz

$F \times G = G \times F$	(32)

Iloczyn zbiorów rozmytych:

Niech $X \in [0,10]$ zaś:

$F = 0,10/1 + 0,20/2 + 0,30/3 + 0,40/4 + 0,30/5 + 0,20/6$	(33)

$G = 0,10/2 + 0,50/3 + 0,70/4 + 1,00/5 + 1,00/6$	(34)

stąd:

$FG = 0,02/2 + 0,15/3 + 0,28/4 + 0,30/5 + 0,20/6$	(35)

Jeśli $F \equiv G$ to Def. 9 określa drugą potęgę zbioru $F$ . Ogólnie:

Potęgę k-tą zbioru rozmytego $F\subseteq X$ oznaczać będziemy jako $F^k$ i definiujemy jako zbiór rozmyty o funkcji przynależności \mu_{F^k}:

$\mu_F^k(x) = \left(\mu_F(x)\right)^k \; ;\;\forall x\in X \; ;\;\ k>0$	(36)

Potęga zbioru rozmytego:

Niech $X \in [0,10]$ , $k=2$ oraz:

$F = 0,10/1 + 0,20/2 + 0,30/3 + 0,40/4 + 0,30/5 + 0,20/6$	(37)

stąd:

$F^k = 0,01/1+ 0,04/2 + 0,09/3 + 0,16/4 + 0,09/5 + 0,04/6$	(38)

Jak już wiemy, parametrem charakterystycznym zbioru rozmytego jest jego wysokość $h(F)$ . Zbiór rozmyty może być scharakteryzowany także przez jego moc (liczbę kardynalną) lub moc kwadratową.

Moc nierozmytą (liczbę kardynalną lub krótko mocą) zbioru rozmytego $F\subseteq X$ rozpiętego na skończonej przestrzeni $X$ o przeliczalnej liczbie elementów $n$ definiujemy jako sumę arytmetyczną postaci:

$\left\vert F\right\vert=\sum_{i=1}^n \mu_F(x_{i}) \; ;\;\forall x\in X$	(39)

Jeśli $\mu_{F}(x)\in [0, 1]$ to jak łatwo zauważyć:

$0\leqslant\left\vert F\right\vert\leqslant n$	(41)

Moc zbioru rozmytego:

Niech $X \in [0,10]$ oraz:

$F = 0,10/1 + 0,20/2 + 0,30/3 + 0,40/4 + 0,30/5 + 0,20/6$	(42)

stąd:

$\|F\| = 0,10 + 0,20 + 0,30 + 0,40 + 0,30 + 0,20 = 1,50$	(43)

Moc nierozmytą kwadratową (kwadratową liczbę kardynalną) zbioru rozmytego $F\subseteq X$ rozpiętego na skończonej przestrzeni $X$ o przeliczalnej liczbie elementów $n$ definiujemy jako sumę arytmetyczną postaci:

$\left\vert F\right\vert^2=\sum_{i=1}^n \left(\mu_F(x_{i})\right)^2 \; ;\;\forall x\in X$	(44)

Jeśli $\mu_{F}(x)\in [0,1]$ to jak łatwo zauważyć:

$0\leqslant\left\vert F\right\vert^2\leqslant n$	(45)

$\left\vert F\right\vert^2\leqslant \left\vert F\right\vert$	(46)

Moc kwadratowa zbioru rozmytego:

Niech $X \in [0,10]$ oraz zbiór $F$ będzie identyczny jak w przykładzie 12:

$F = 0,10/1 + 0,20/2 + 0,30/3 + 0,40/4 + 0,30/5 + 0,20/6$	(47)

stąd:

$\|F\|^2= 0,01 + 0,04 + 0,09 + 0,16 + 0,09 + 0,04 = 0,43$	(48)

Dopełnienie bezwzględne zbioru rozmytego $F\subseteq X$ w przestrzeni rozważań $X=\left\{x\right\}$ oznaczać będziemy jako $\neg F$ i definiować jako:

$\mu_{\neg F}(x)= 1-\mu_F(x)\; ;\;\forall x\in X; \mu_F(x)\in[0,1]$	(49)

Dopełnienie zbioru rozmytego:

Niech $X \in [0,10]$ oraz $F$ będzie identyczne jak w przykładzie 12:

$F = 0,10/1 + 0,20/2 + 0,30/3 + 0,40/4 + 0,30/5 + 0,20/6$	(47)

stąd:

$\neg F= 0,90/1 + 0,80/2 + 0,70/3 + 0,60/4 + 0,70/5 + 0,80/6$	(48)

Jak łatwo zauważyć, funkcja przynależności zbioru rozmytego i jej dopełnienie są zwierciadlanymi odbiciami względem prostej $\mu (x)=0,5$ (por. Rys. 8). Ponadto można zauważyć, że:

${\neg \textbf 0=\textbf 1}$	(52)

oraz

${\neg \textbf 1=\textbf 0}$	(53)

Przykład funkcji przynależności... — Rys. 8. Przykład funkcji przynależności $\mu_{WM}(x)$ zbioru rozmytego $WM$ (*"wysoki mężczyzna"*) oraz dopełnienia tego zbioru $\neg WM$ (*"nie wysoki mężczyzna"*)

Rys. 8. Przykład funkcji przynależności $\mu_{WM}(x)$ zbioru rozmytego $WM$ (*"wysoki mężczyzna"*) oraz dopełnienia tego zbioru $\neg WM$ (*"nie wysoki mężczyzna"*)

Sumę mnogościową zbiorów rozmytych $F,G\subseteq X$ , oznaczać będziemy jako $F+G$ lub $F\cup G$ . Funkcję przynależności tego zbioru definiujemy jako obwiednię maksymalnych wartości funkcji przynależności obu zbiorów:

$\mu_{F\cup G}(x) = \mu_{F}(x)\cup\ \mu_{G}(x)\; ;\;\forall x\in X$	(49)

gdzie symbol $\cup$ oznacza operację maksimum.

Z (54) wynika, że:

$\textbf 0 \cup \textbf 0=\textbf 0$	(55)

$\textbf 0 \cup \textbf 1=\textbf 1$	(56)

$\textbf 1 \cup \textbf 0=\textbf 1$	(57)

$\textbf 1 \cup \textbf 1=\textbf 1$	(58)

$F\cup F= F$	(59)

$F \cup \textbf 0 = F$	(60)

$F \cup \textbf 1 = \textbf 1$	(61)

$\neg F \cup \neg F = \neg F$	(62)

Właściwości (55...62) są co do ogólnej formy zapisu zgodne z analogicznymi zapisami logiki boolowskiej. Jak łatwo wywieść, suma mnogościowa charakteryzuje się właściwościami przemienności (63) i łączności (64).

$F\cup G = G\cup F$	(63)

$\left(F\cup G\right) \cup H= F\cup \left(G \cup H\right)$	(64)

Suma mnogościowa zbiorów rozmytych:

Niech $X \in [0,10]$ oraz $F$ będzie identyczne jak w przykładzie 12:

$\quad\quad F \quad\quad=0,1/1 + 0,2/2 + 0,3/3 + 0,4/4 + 0,3/5 + 0,2/6$	(65)

oraz:

$\quad\quad G\quad\quad =0,2/1 + 0,8/2\quad\quad\quad\;\,\, +1,0/4 + 0,1/5 + 0,2/6$	(66)

stąd:

$\quad\quad F\cup G\, = 0,2/1 + 0,8/2 + 0,3/3 + 1,0/4 + 0,3/5 + 0,2/6$	(67)

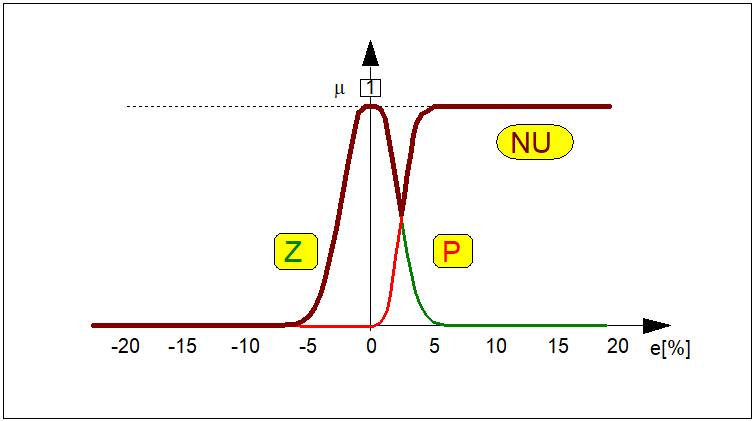
Interpretacja graficzna zbioru rozmytego... — Rys. 9. Interpretacja graficzna operacji sumy mnogościowej zbioru rozmytego $Z$ (*"zerowa odchyłka regulacji"*) oraz $\mu P(x)$ zbioru rozmytego $P$ (*"dodatnia odchyłka regulacji"*). Suma mnogościowa może być interpretowana jako rozmyty zbiór o etykiecie lingwistycznej $NU$ (*"nieujemna odchyłka regulacji"*).

Rys. 9. Interpretacja graficzna operacji sumy mnogościowej zbioru rozmytego $Z$ (*"zerowa odchyłka regulacji"*) oraz $\mu P(x)$ zbioru rozmytego $P$ (*"dodatnia odchyłka regulacji"*). Suma mnogościowa może być interpretowana jako rozmyty zbiór o etykiecie lingwistycznej $NU$ (*"nieujemna odchyłka regulacji"*).

Przecięcie mnogościowe zbiorów rozmytych $F,G\subseteq X$ oznaczać będziemy jako $F\cap G$ . Funkcję przynależności tego zbioru definiujemy jako obwiednię minimalnych wartości funkcji przynależności obu zbiorów:

$\mu_{F\cap G}(x) = \mu_{F}(x)\cap\ \mu_{G}(x)\; ;\;\forall x\in X$	(68)

Z (68) wynika, że:

$\textbf 0 \cap \textbf 0=\textbf 0$	(69)

$\textbf 0 \cap \textbf 1=\textbf 0$	(70)

$\textbf 1 \cap \textbf 0=\textbf 0$	(71)

$\textbf 1 \cap \textbf 1=\textbf 1$	(72)

$F\cap F= F$	(73)

$F \cap \textbf 0 = \textbf 0$	(74)

$F \cap \textbf 1 = \textbf 1$	(75)

$\neg F \cap \neg F = \neg F$	(76)

Zapisy (69..76) są co do ogólnej formy zgodne z analogicznymi zapisami algebry boolowskiej. Jak łatwo wywieść przecięcie mnogościowe, podobnie jak suma mnogościowa, charakteryzuje się właściwościami przemienności (77) i łączności (78).

$F\cap G = G\cap F$	(77)

$\left(F\cap G\right) \cap H= F\cap \left(G \cap H\right)$	(78)

Przecięcie mnogościowe zbiorów rozmytych:

Niech $X \in [0,10]$ oraz $F$ i $G$ będą identyczne jak w przykładzie 15:

$\quad\quad F \quad\quad=0,1/1 + 0,2/2 + 0,3/3 + 0,4/4 + 0,3/5 + 0,2/6$	(79)

oraz:

$\quad\quad G\quad\quad =0,2/1 + 0,8/2\quad\quad\quad\;\,\, +1,0/4 + 0,1/5 + 0,2/6$	(80)

stąd:

$\quad\quad F\cap G\, = 0,1/1 + 0,2/2 + 0,0/3 + 0,4/4 + 0,1/5 + 0,2/6$	(81)

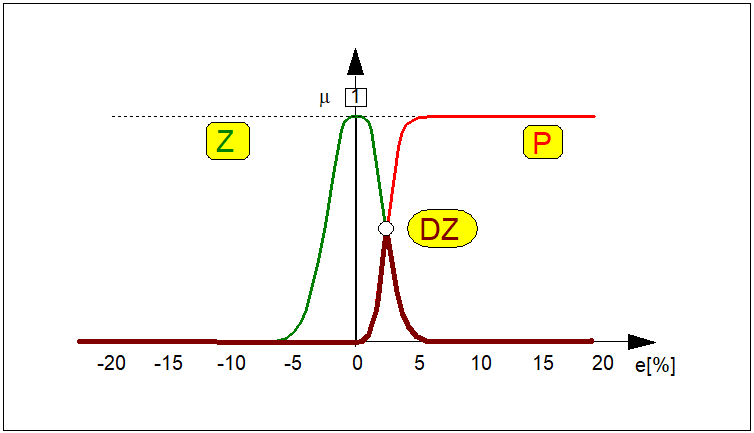
nterpretacja graficzna przecięcia mnogościowego... — Rys. 10. Interpretacja graficzna przecięcia mnogościowego: zbioru rozmytego $Z$ (*"zerowa odchyłka regulacji"*) oraz $\mu_P(x)$ zbioru rozmytego $P$ (*"dodatnia odchyłka regulacji"*). Przecięcie mnogościowe może być interpretowane jako rozmyty zbiór o etykiecie lingwistycznej $ZD$ (*"zerowa i dodatnia odchyłka regulacji"*). Należy zwrócić uwagę na rozmyty charakter zbioru $ZD$ niemożliwy do przyjęcia na gruncie klasycznej (nierozmytej) teorii mnogości.

Rys. 10. Interpretacja graficzna przecięcia mnogościowego: zbioru rozmytego $Z$ (*"zerowa odchyłka regulacji"*) oraz $\mu_P(x)$ zbioru rozmytego $P$ (*"dodatnia odchyłka regulacji"*). Przecięcie mnogościowe może być interpretowane jako rozmyty zbiór o etykiecie lingwistycznej $ZD$ (*"zerowa i dodatnia odchyłka regulacji"*). Należy zwrócić uwagę na rozmyty charakter zbioru $ZD$ niemożliwy do przyjęcia na gruncie klasycznej (nierozmytej) teorii mnogości.

Na definicji 14 oparta jest definicja implikacji znanej w literaturze z dziedziny sterowania rozmytego implikacją Mamdaniego. Implikacja Mamdaniego jest relacją wzajemną zbiorów rozmytych. Została ona zdefiniowana według zasady minimum. Oznacza to, że każdy element każdego zbioru jest w relacji z każdym elementem innego zbioru. Według rozmytej implikacji Mamdaniego każdej takiej relacji przypisywana jest wartość równa minimalnej wartości funkcji przynależności spośród elementów, dla których jest wyznaczana.

Relacja rozmyta $Rc$ zbiorów rozmytych $F\subseteq X$ , $G\subseteq Y$ w ujęciu Mamdaniego, jest zdefiniowana jako hiperpowierzchnia rozpięta nad iloczynem kartezjańskim suportów zbiorów będących w relacji z punktami wsparcia o wartościach wyznaczonymi zgodnie z definicją przecięcia wartości funkcji przynależności.

$\mu_{R_{c}}(x,y) = \mu_{F}(x)\cap\ \mu_{G}(y)\; ;\;\forall x\in X\; ;\;\forall y\in Y$	(82)

Implikacja Mamdaniego:

Niech $X,Y\in [0, 10]$ oraz $F$ i $G$ będą następujące:

$F = 0,1/1 + 0,2/2 + 0,3/3$	(83)

oraz:

$G= \quad\quad\quad\;\;\:0,2/4 + 0,8/5$	(84)

Suportami obu zbiorów są odpowiednio:

$Support(F) =\left\{1, 2, 3\right\}$

$Support(G) =\left\{4, 5\right\}$

Iloczyn kartezjański suportów $F \times G =\left\{1,4 1,5 2,4 2,5, 3,4 3,5\right\}$

stąd:

$R_{c} (F,G)=0,1/1,4+0,1/1,5+0,2/2,4+0,2/2,5+0,2/3,4+0,3/3,5$	(85)

Relację $R_c(F,G)$ można dla przejrzystości przedstawić w postaci tabelarycznej

Tabela 1: Ilustracja przykładu 17 w postaci tabelarycznej
$R_C(F,G)$	$F$
G	1	2	3
4	0,1	0,2	0,2
5	0,1	0,2	0,3

lub w postaci reguł typu jeżeli to, np:

$\begin{array}{c} \textbf{jezeli}\; (x=1 \cap y=4)\; \textbf{to}\; (Rc (F,G) = 0,1)\; \textbf{inaczej}\\ \textbf{jezeli}\; (x=1 \cap y=5)\; \textbf{to}\; (Rc (F,G) = 0,1)\; \textbf{inaczej} \\ \textbf{jezeli}\; (x=2 \cap y=4)\; \textbf{to}\; (Rc (F,G) = 0,2)\; \textbf{inaczej} \\ \textbf{jezeli}\; (x=2 \cap y=5)\; \textbf{to}\; (Rc (F,G) = 0,2)\; \textbf{inaczej} \\ \textbf{jezeli}\; (x=3 \cap y=4)\; \textbf{to}\; (Rc (F,G) = 0,2)\; \textbf{inaczej} \\ \textbf{jezeli}\; (x=3 \cap y=4)\; \textbf{to}\; (Rc (F,G) = 0,3)\;.\quad\quad\quad \end{array}$ (86)

Jak można zauważyć z (86) implikacja jest w istocie metodą wnioskowania bazującą na zbiorze reguł warunkowych. Wniosek wynikający z każdej reguły jest uwarunkowany wartością przesłanki. Zatem, aby mógł być wywiedziony wniosek, konieczne jest wyznaczenie wartości tej przesłanki. W przypadku relacji rozmytej w ujęciu Mamdaniego zarówno przesłanka jak i wniosek mają charakter rozmyty.