Podręcznik: Model analityczny

3. Modelowanie rozmyte

3.2. Model analityczny

Podejście klasyczne polega na wyznaczeniu modelu matematycznego obiektu i doborze układu regulacji z uwzględnieniem zdefiniowanych kryteriów jakości.

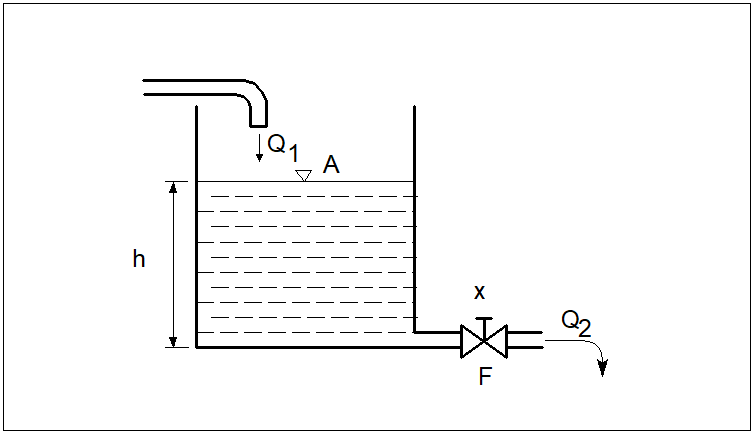
Rys. 11. Szkic fragmentu układu regulacji wysokości słupa cieczy w zbiorniku.
Oznaczenia: $A$ - powierzchnia zbiornika, $h$ - wysokość słupa cieczy, $Q_1$ - strumień objętościowy cieczy dopływającej, $Q_2$ - strumień objętościowy cieczy wypływającej, $x$ - stopień otwarcia zaworu dławiącego wypływ, $F$ - powierzchnia przepływowa zaworu.

Rys. 11. Szkic fragmentu układu regulacji wysokości słupa cieczy w zbiorniku.
Oznaczenia: $A$ - powierzchnia zbiornika, $h$ - wysokość słupa cieczy, $Q_1$ - strumień objętościowy cieczy dopływającej, $Q_2$ - strumień objętościowy cieczy wypływającej, $x$ - stopień otwarcia zaworu dławiącego wypływ, $F$ - powierzchnia przepływowa zaworu.

Załóżmy, że wielkością wejściową jest stopień otwarcia $x$ zaworu dławiącego wypływ ze zbiornika, zaś wielkością wyjściową jest wysokość słupa cieczy $h$ . W podejściu klasycznym, przy zastosowaniu opisu liniowego, poszukiwana jest transmitancja operatorowej obiektu $G(s)$ w postaci:

$G(s)= \frac{H(s)}{X(s)}$	(87)

gdzie:
$H(s)$ - transformata Laplace'a sygnału wyjściowego
$X(s)$ - transformata Laplace'a sygnału wejściowego

Załóżmy dalej, dla uproszczenia, że $Q_1 = const$ .

Zmiana wysokości słupa cieczy $\delta h$ wynika z różnicy strumieni objętościowych: cieczy wpływającej $Q_1$ i wypływającej $Q_2$ :

$A\Delta h =\Delta t (Q_1 - Q_2)$	(88)

Strumień objętościowy $Q_2$ można wyrazić w postaci:

$Q_2 =\alpha \cdot x \cdot \sqrt {2gh}$	(89)

gdzie:
$\alpha$ - współczynnik przepływu
$g$ - przyśpieszenie ziemskie

Po linearyzacji, nieliniowej względem $h$ , zależności (89) w otoczeniu punktu $h_o$ , $x_o$ otrzymujemy:

$\Delta Q_2 =\left\vert{\frac{\partial Q_2}{\partial x}}\right\vert _{x=x_o}\Delta x+\left\vert{\frac{\partial Q_2}{\partial h}}\right\vert _{h=h_o}\Delta h$	(90)

a zatem:

$\Delta Q_2 =\alpha \cdot \sqrt {2gh_{0}}\cdot \Delta x +x_{0}\cdot\alpha \cdot\sqrt {\frac{g}{2h_0}}\cdot\Delta h$	(91)

podstawiając:

$k_1 =\alpha \cdot \sqrt {2gh_{0}}\;\;\;\; ; \quad k_2=x_{0}\cdot\alpha \cdot\sqrt {\frac{g}{2h_0}}$	(92)

otrzymujemy zlinearyzowaną postać na $\Delta Q_2$ :

$\Delta Q_2 =k_{1}\cdot \Delta x +k_{2}\cdot\Delta h$	(93)

Przedstawiając równanie (88) w formie równania różnicowego otrzymujemy:

$A\Delta(\Delta h) =\Delta t (\Delta Q_1 - \Delta Q_2)$	(94)

a ponieważ $Q_1 = const$ oraz po uwzględnieniu (93) otrzymujemy:

$A\Delta(\Delta h) =-\Delta t\cdot k_{1}\cdot\Delta x -\Delta t\cdot k_{2}\cdot\Delta h$	(95)

Stąd w granicy dla $t\rightarrow 0$

$A\Delta h =- k_{1}\cdot\Delta x - k_{2}\cdot\Delta h$	(96)

Oznaczając: $H(s) = L\left\{\Delta h\right\}$ oraz $X(s) = L\left\{x\right\}$ otrzymujemy ostatecznie:

$G(s)= \frac{H(s)}{X(s)}=-\frac{k}{Ts+1}$	(97)

gdzie: $T = A / k_2$ ; $k= k_1 / k_2$

Jak łatwo zauważyć transmitancja operatorowa (97) ma postać właściwą elementowi inercyjnemu rzędu pierwszego. Znak minus poprzedzający transmitancję należy interpretować w ten sposób, że wzrost stopnia otwarcia zaworu $x$ na wypływie powoduje spadek, a nie wzrost wielkości wyjściowej jaką jest wysokość słupa cieczy $h$ .

Transmitancja (97) jest bardzo wygodna do prowadzenia analizy właściwości dynamicznych obiektu, doboru układu regulacji, badania stabilności, itp. Wartości współczynników $k_1$ i $k_2$ są jednak zależne od wyboru punktu pracy. Wartości te mogą być traktowane jako wartości stałe tylko w niewielkim otoczeniu punktu pracy $(x_o , h_o )$ .

W praktyce uzyskanie modeli analitycznych obiektów sterowania nie jest proste. Wynika to głównie ze złożoności procesów zachodzących w rzeczywistych obiektach, niemożliwości zastosowania opisu liniowego, braku dostatecznej wiedzy co do wartości parametrów opisujących proces, konieczności przeprowadzenia kosztownej identyfikacji parametrów modelu, itp. W takich sytuacjach należy rozważyć opis jakościowy procesu możliwy do uzyskania na podstawie wiedzy heurystycznej, wiedzy uzyskanej z eksperymentu myślowego lub wiedzy eksperckiej.