Podręcznik

Proces wnioskowania rozmytego może być przedstawiony w trzech alternatywnych formach: albo w postaci relacji (implikacji) rozmytej albo w postaci zdań warunkowych albo w postaci tabeli sterowań rozmytych.

Jak już wspomniano wcześniej, implikacja może być interpretowana jako metoda wnioskowania bazującą na zbiorze alternatywnych reguł warunkowych. Stąd nasuwa się wniosek, że proces wnioskowania rozmytego można wyrazić w postaci zbioru alternatywnych reguł warunkowych.

Każda reguła warunkowa definiuje warunek, który wymaga spełnienia aby wniosek wypływający z reguły był prawdziwy. Notacja reguły warunkowej składa się z dwóch słów kluczowych, przesłanki i wniosku.

$\textbf{jeżeli} \langle przesłanka \rangle \textbf{to} \langle wniosek \rangle$

Przesłanka reguły bywa także nazywaną poprzednikiem reguły lub premisą, a wniosek bywa nazywany konkluzją reguły.

W odróżnieniu od reguły klasycznej (ostrej), reguła rozmyta na podstawie rozmytej przesłanki określa nie tyle prawdziwość lub nieprawdziwość wniosku lecz stopień jego spełnienia. Stopień spełnienia wniosku zdefiniowany jest w zakresie liczbowym $[0..1]$. Stopień ten można interpretować w taki sposób, że jeśli przyjmuje on wartość zerową to wniosek wynikający z tej reguły nie jest spełniony, jeśli przyjmuje wartość równą jeden, to jest spełniony w stopniu najwyższym, jeśli przyjmuje wartość pośrednią pomiędzy zerem i jedynką to jest spełniony częściowo.

Należy wspomnieć, że zależnie od definicji implikacji rozmytej, wniosek może ale nie musi mieć postaci rozmytej. Implikacja Mamdaniego na podstawie rozmytych przesłanek przyporządkuje stopień spełnienia rozmytych wniosków. Z kolei implikacja Takagi-Sugeno na podstawie rozmytych przesłanek przyporządkuje stopień spełnienia wniosku ostryego.

W szczególności implikacja rozmyta może być wykorzystana do sterowania np. w ten sposób, że rozmytej odchyłce sterowania przyporządkowuje rozmyty sygnał nastawiający regulatora. Bezpośrednie zastosowanie implikacji rozmytej do konstrukcji regulatorów jest o tyle trudne, że w praktyce zarówno wejścia regulatora jak i jego wyjścia mają raczej charakter ostry, a nie rozmyty. Stwierdzenie to można uogólnić, ponieważ dotyczy nie tylko sterowania lecz także zdecydowanej większości zastosowań metod logiki rozmytej w praktyce.

Praktyczne wykorzystanie rachunku zbiorów rozmytych wymaga zatem zastosowania dwóch dodatkowych przekształceń:

1. przekształcenia wejść ostrych do postaci rozmytej,
2. przekształcenia rozmytego wyjścia regulatora do postaci ostrej.

Pierwsze przekształcenie nosi nazwę operacji rozmywania lub fuzyfikacji. Drugie przekształcenie nosi nazwę operacji wyostrzania lub defuzyfikacji.

Operację przekształcenia wejść rozmytych w wyjścia rozmyte nazywać będziemy dalej operacją wnioskowania lub inferencji rozmytej. Realizacja operacji związanych z rozmywaniem wejść i wyostrzaniem wyjść jest kosztowna czasowo. Czas realizacji tych operacji, w tym zwłaszcza operacji wyostrzania nie jest bez znaczenia w zastosowaniach krytycznych czasowo.

Na rysunku poniżej przedstawiono ogólny schemat wnioskowania rozmytego stosowany w zastosowaniach praktycznych.

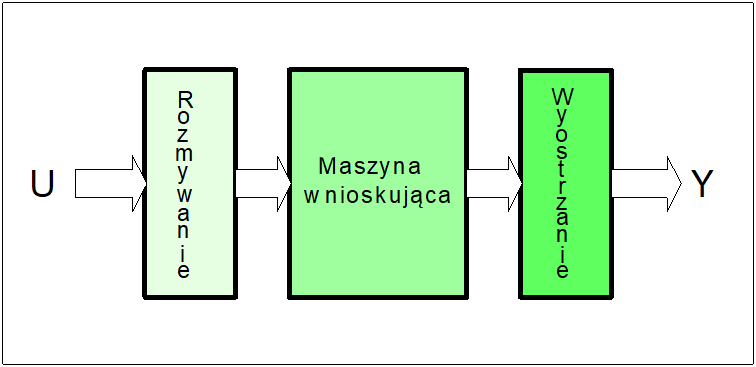
W nielicznych przypadkach praktycznych operacja wyostrzania wniosków rozmytych nie jest stosowana. Dotyczy to np. zastosowania logiki rozmytej w diagnostyce procesów do realizacji zadania lokalizacji uszkodzeń. W tym przypadku wyjściem procesu wnioskowania są rozmyte stopnie wystąpienia poszczególnych uszkodzeń. Stopnie te wyznaczane są na podstawie reguł, których przesłankami są wartości rozmyte sygnałów diagnostycznych właściwych każdemu uszkodzeniu. Agregacja wszystkich wniosków (stopni) w procesie wyostrzania, w tym przypadku nie ma większego sensu.