Podręcznik

Metoda środka sum (COS) jest metodą pokrewną do metody środka ciężkości. W metodzie COG wyznaczenie wartości ostrej (poza przypadkami szczególnymi) wymaga poniesienia dość intensywnych nakładów mocy obliczeniowych (por. wzór 109). Znacznie prostsze implementacyjnie rozwiązanie problemu wyostrzania uzyskać można stosując metodę wyznaczania środka ciężkości znając współrzędne wszystkich środków ciężkości wszystkich wniosków cząstkowych wynikających ze wszystkich reguł. Jak dowiemy się o tym później, ten sposób jest stosowany do wyostrzania wniosków w aproksymatorze Takagi-Sugeno.

Na dobrą sprawę, także taki sposób został zastosowany w przykładzie 22 w celu wyznaczenia środka ciężkości dla szczególnej (singletonowej) postaci funkcji przynależności wniosku. Powstaje jednak pytanie czy w przypadku ogólnym wynik wyostrzania metodą środka sum jest równoważny wynikowi uzyskiwanemu metodą środka obszaru? Odpowiedź na to pytanie jest negatywna. A skoro tak jest, to pojawia się następne pytanie czy wynik wyostrzania zależy nie tylko od wyostrzanej funkcji przynależności, ale także od użytej metody wyostrzania? Odpowiedź w tym przypadku jest niepokojąco pozytywna. W tym miejscu u czytelnika powstaje zapewne wątpliwość jaki ma sens wprowadzanie innych metod wyostrzania i czy mają one jakieś znaczenie praktyczne? Otóż odpowiedź na to pytanie jest dość prosta. Wszystkie metody wyostrzania przedstawione dalej w tym skrypcie zostały zaprojektowane tylko w jednym celu, a mianowicie po to aby zmniejszyć koszt obliczeniowy w stosunku do metody COG. Niestety odbyło się to kosztem zwiększenia niepewności wyznaczenia wniosku ostrego. Problem ten będzie szerzej skomentowany na zakończenie tego podrozdziału.

W metodzie środka sum milcząco zakłada się, że uzyskanie dobrego efektu zmniejszenia mocy obliczeniowej można uzyskać w przypadku, gdy funkcje przynależności wniosków cząstkowych mają postać prostych figur geometrycznych. Założenie takie nie jest bezpodstawne, bowiem w praktyce dość powszechnie stosowane są proste funkcje przynależności o kształcie trójkątnym (typ $\Delta$) lub trapezowym (typ $\Pi$), dla których wyznaczenie środka ciężkości obszaru jest trywialne.

Ponadto warto zauważyć, że wnioski z reguł cząstkowych mają bardzo często kształt trapezowy i to niezależnie od tego, czy funkcje przynależności wniosków cząstkowych projektowane są w postaci trójkątów, czy trapezów. Jest to widoczne między innymi na Rys. 18. Funkcje trapezowe wniosków cząstkowych powstają w wyniku efektu „przycinania” pierwotnych funkcji przynależności tych wniosków na poziomie zapłonu reguły. W tym przypadku efekt „przycięcia” przekształca trójkąty w trapezy i trapezy w trapezy.

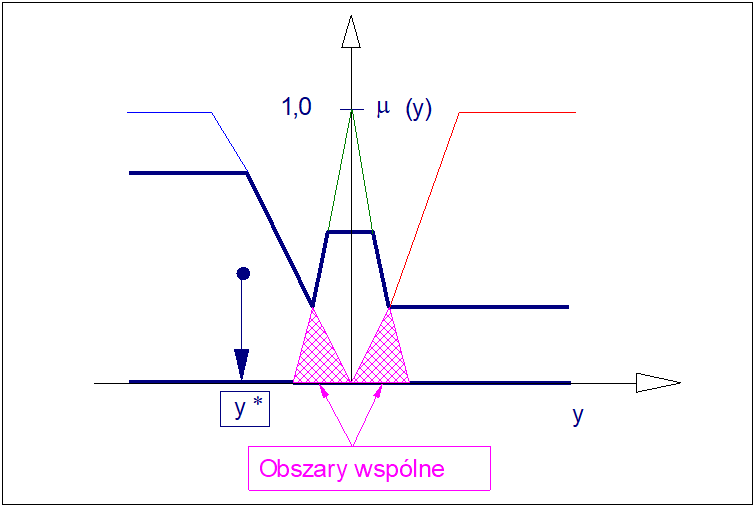
Rozbieżność wyników wyostrzania uzyskiwanych metoda COG i COS można wyjaśnić następująco. W metodzie COG obszary wspólne wszystkich wniosków cząstkowych (dla których istnieją przecięcia niezerowe) podlegają agregacji metodą sumy mnogościowej. Zatem w tej metodzie są uwzględniane tylko raz do wyznaczenia wartości ostrej $y^*$. W przypadku metody COS obszary wspólne wniosków cząstkowych są uwzględniane tyle razy ile razy występują niezerowe przecięcia tych wniosków. Jeśli zatem wnioski cząstkowe mają wyłącznie przecięcia puste (jak np. w przypadku funkcji przynależności zbiorów singletonowych (por. Rys. 20) to metody wyostrzania COG i COS generują identyczne wyniki. Ze względu na prostotę, algorytm wyostrzania metodą COS jest dość powszechnie stosowany w praktyce. W ogólnym przypadku wartość ostrą z $n$ wniosków cząstkowych wyznaczyć można znając współrzędne środków ciężkości tych wniosków:

gdzie: $[y_i^*,\mu_i^*]$ - współrzędne wniosku ostrego i-tej reguły cząstkowej.

Łatwo zauważyć podobieństwo postaci wzorów (112) i (113). Można je wyjaśnić w ten sposób, że metoda środka sum w istocie dokonuje transformacji funkcji przynależności wniosków z reguł cząstkowych do postaci singletonowej.

Ilustrację problemu wielokrotnego uwzględniania obszarów o przecięciu niezerowym w wyznaczeniu wniosku ostrego ze zbioru reguł rozmytych metodą środka ciężkości sum (COS) przedstawiono na rysunku poniżej.