Podręcznik

Niewątpliwie najbardziej spektakularnym osiągnięciem teorii zbiorów rozmytych w teorii sterowania było wprowadzenie i zastosowanie regulatorów rozmytych. Regulatory rozmyte znajdują obecnie liczne zastosowania przemysłowe i komercyjne. Stosowane są powszechnie do sterowania procesów silnie nieliniowych.

W tym rozdziale omówimy podejścia do konstrukcją wybranych rozmytych algorytmów regulacyjnych. Dla skoncentrowania uwagi w dalszym ciągu będziemy zajmować się regulatorami przeznaczonymi do zastosowań w jednoobwodowych układach regulacji z ujemnym sprzężeniem zwrotnym. Schemat blokowy takiego układu przedstawiono na rysunku poniżej.

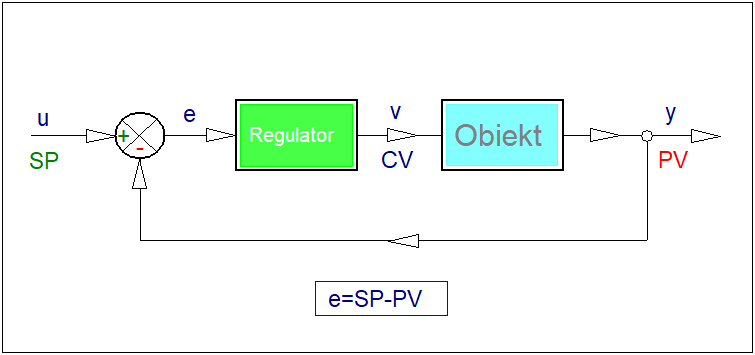
W układzie sterowania automatycznego odchyłka regulacji jest miarą różnicy pomiędzy wartością zadaną (pożądaną), a wartością mierzoną (rzeczywistą) na wyjściu obiektu regulacji. Do konstrukcji algorytmów regulacji rozmytej istotne jest oczywiste, aczkolwiek ważne spostrzeżenie, że ujemna wartość odchyłki regulacji oznacza, że wartość mierzona ma wartość zbyt wysoką i odwrotnie: dodatnia wartość odchyłki regulacji wskazuje, że wartość mierzona jest zbyt mała. W przypadku odchyłki ujemnej regulator powinien kształtować w taki sposób sterowanie CV, aby sprowadzić odchyłkę regulacji do wartości zerowej lub przynajmniej bliskich zeru. W najprostszym przypadku jeśli odchyłka regulacji jest ujemna, to regulator powinien skompensować ją przez zmniejszenie sygnału sterowania CV, jeśli odchyłka jest zerowa, to regulator nie powinien zmieniać sygnału sterującego, jeśli odchyłka jest dodatnia to powinien zwiększyć sterowanie. Łatwo zwrócić uwagę, że w ten sposób dokonaliśmy lingwistycznego opisu pewnego, dobrze znanego regulatora o działaniu bezinercyjnym. Szczególnym przypadkiem takiego regulatora jest regulator typu P.

Syntezę regulatorów rozmytych będziemy realizowali zgodnie z przedstawioną w podrozdziale 3.1 metodyką projektowania modeli rozmytych. Metodykę projektowania regulatorów rozmytych można scharakteryzować w postaci sześciu zasadniczych kroków:

Krok 1 (formalny)

Każdej zmiennej ostrej (zarówno wejściowej jak i wyjściowej) przyporządkować nazwę lingwistyczną.

Krok 2 (projekt zbiorów rozmytych)

Każdej zmiennej lingwistycznej przyporządkować wartości w postaci znormalizowanych zbiorów rozmytych.

Krok 3 (projekt bazy reguł)

Na podstawie wiedzy matematycznej, heurystycznej, eksperckiej, doświadczalnej, sformułować relacje rozmyte wiążące wejścia i wyjścia.

Krok 4 (wyznaczenie wartości rozmytej wejść)

Na podstawie znajomości wartości wejść ostrych oraz znajomości zbiorów rozmytych wejść (krok 2) wyznaczyć zbiór wartości funkcji przynależności każdej zmiennej lingwistycznej odpowiadający wartościom ostrym wejść.

Krok 5 (wyznaczenie wartości rozmytej wyjść)

Na podstawie znajomości wartości rozmytych wejść (krok4) oraz relacji (krok 3) wyznaczyć zbiór wartości funkcji przynależności każdej zmiennej lingwistycznej wyjścia.

Krok 6 (wyznaczenie wartości wyjść ostrych)

Na podstawie znajomości wartości wyjść rozmytych stosując odpowiednią metodę wyostrzania wyznaczyć wartości ostre wyjścia.

Pozostaje sprawą dyskusyjną, czy zastosowanie tak złożonej procedury do realizacji prostego liniowego regulatora typu P ma jakikolwiek sens praktyczny?

Znacznie prościej regulator taki realizowany jest metodami właściwymi podejściom ostrym. Jakkolwiek odpowiedź na to pytanie w przypadku realizacji nieliniowego rozmytego regulatora bezinercyjnego typu P nie jest już tak jednoznaczna.