Podręcznik
Wstęp do logiki rozmytej
4. Przykłady regulatorów rozmytych
4.1. Rozmyty regulator typu P
Do syntezy rozmytego regulatora typu P zastosujmy przedstawiony wyżej algorytm złożony z sześciu kroków.
Krok 1 (formalny)
Rozważmy regulator typu P o strukturze SISO. Wejściem regulatora jest sygnał odchyłki regulacji \( e \), a jego wyjściem jest sygnał sterujący (nastawiający) \( v \). Oba sygnały są wielkościami ostrymi, których wartości należą do znormalizowanych przedziałów \( [-1, 1] \).
Następnie przyporządkujmy odchyłce regulacji \( e \) nazwę lingwistyczną <odchyłka regulacji>, oraz sygnałowi sterującemu v nazwę lingwistyczną <sygnał sterujący>. W celu skrócenia notacji, w dalszym ciągu będziemy stosowali nazwy alternatywne e i v odpowiednio dla <odchyłki regulacji> i <sygnału sterującego>.
Następnie zmiennej <odchyłka regulacji> przyporządkujemy dwie wartości <odchyłka ujemna> i <odchyłka dodatnia>. Wartościom tym nadano alternatywne nazwy: \( N_e \) i \( P_e \). W podobny sposób zmiennej <sygnał sterujący> przyporządkujemy dwie wartości <zmniejsz sterowanie> i <zwiększ sterowanie>. Wartościom tym nadano odpowiednio krótsze alternatywne nazwy symboliczne \( N_s \) i \( P_s \). Wartości \( N_e \) , \( P_e \) , \( N_s \) i \( P_s \) są już zbiorami rozmytymi, których funkcje przynależności zostaną zdefiniowane w następnym kroku.
Krok 2 (projekt zbiorów rozmytych)
Projekt zbiorów rozmytych \( N_e \) , \( P_e \) , \( N_s \) i \( P_s \) przedstawiony został w formie graficznej na Rys. 29. Wszystkie funkcje przynależności wszystkich zbiorów zdefiniowano w znormalizowanej i ograniczonej obustronnie przestrzeni rozważań \( [-1,1] \). Zbiory rozmyte reprezentujące wartości rozmytego sygnału wejściowego zaprojektowano w postaci dwóch symetrycznych funkcji trójkątnych. Natomiast wyjście rozmyte zaprojektowano w postaci zbiorów singletonowych. Dzięki temu, (jak wiemy z rozdziału 3) możliwe jest znakomite uproszczenie procesu wyostrzania. W ogólności funkcje przynależności wartości wejść i wyjść mogą mieć dowolne kształty. Z punktu widzenia formalnego ważne jest jedynie to aby zbiory te były zbiorami znormalizowanymi.
Krok 3 (projekt bazy reguł)
Na podstawie analizy przeprowadzonej w komentarzu do Rys. 28, bazę reguł w postaci tabeli sterowań rozmytych regulatora bezinercyjnego o działaniu P przedstawiono w Tabeli 5.
| Reguła | \( e \) | \( y \) |
|---|---|---|
| 1 | \( N_e \) | \( N_s \) |
| 2 | \( P_e \) | \( P_s \) |
Kroki 4, 5, 6 (wyznaczenie wartości rozmytej wejść, wartości rozmytej wyjść i wartości wyjść ostrych)
Na podstawie znajomości wartości wejść ostrych, znajomości zbiorów rozmytych wejść (krok 2) oraz znajomości tabeli reguł (krok 3) wyznaczamy wyjścia ostre stosując metodę środka ciężkości obszaru (COG). Metoda ta, ze względu na dobór charakterystycznych funkcji przynależności wyjścia rozmytego (singletony), jest w naszym przypadku równoważna metodom COS i HM. W Tabeli 6 przedstawiono przebieg procesu wnioskowania rozmytego dla wartości odchyłki regulacji w zakresie jej zmienności w granicach [-1,1].
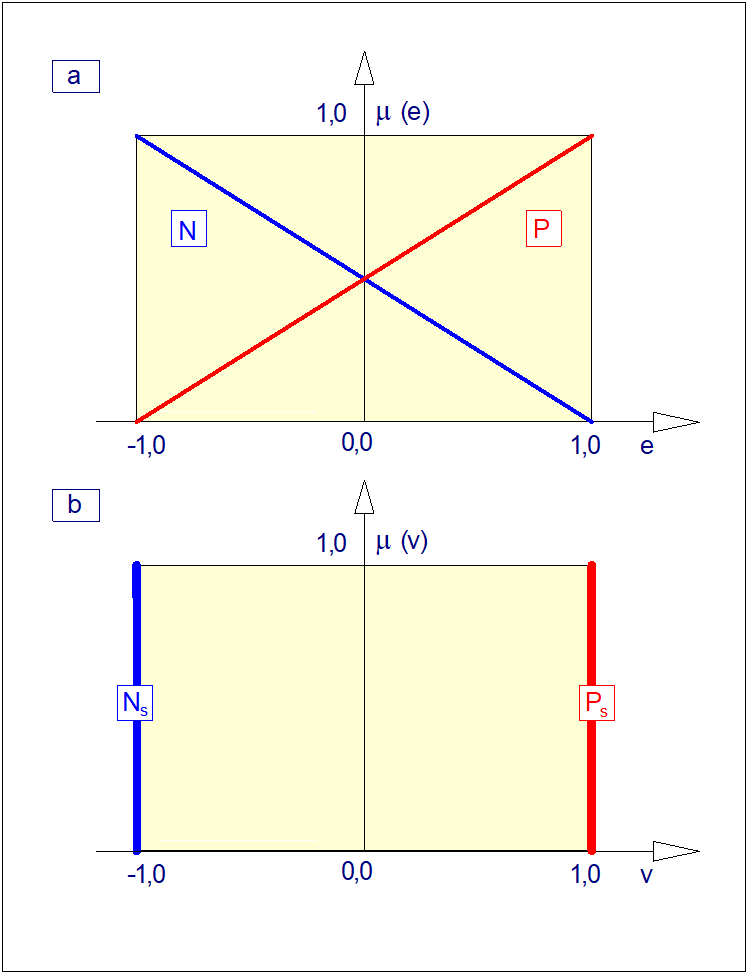
a) Funkcje przynależności wejścia \( e \)
b) Funkcje przynależności wyjścia \( v \)
| \( e \) | \( \mu_N(e) \) | \( \mu_P(e) \) | \( \mu_{N_s}(v) \) | \( \mu_{P_s}(v) \) | \( v \) |
|---|---|---|---|---|---|
| -1,00 | 1,00 | 0,00 | 1,00 | 0,00 | -1,00 |
| -0,75 | 0,88 | 0,13 | 0,88 | 0,13 | -0,75 |
| -0,50 | 0,74 | 0,25 | 0,75 | 0,25 | -0,50 |
| -0,25 | 0,63 | 0,38 | 0,63 | 0,38 | -0,25 |
| 0,00 | 0,50 | 0,50 | 0,50 | 0,50 | 0,00 |
| 0,25 | 0,38 | 0,63 | 0,38 | 0,63 | 0,25 |
| 0,50 | 0,25 | 0,75 | 0,25 | 0,75 | 0,50 |
| 0,75 | 0,13 | 0,88 | 0,13 | 0,88 | 0,75 |
| 1,00 | 0,00 | 1,00 | 0,00 | 1,00 | 1,00 |
| Wejście | Rozmywanie | Wnioskowanie | Wyjście | ||
Zależność \( v = f(e) \) nazywać będziemy funkcją lub charakterystyką sterowania. Dla przypadku wielowymiarowego gdy \( v = f(e) \) zdefiniujemy pojęcia tzw. powierzchni i przestrzeni sterowania.
Powierzchnią sterowania będziemy określali hiperpowierzchnię rozpiętą w przestrzeni (n+1) wymiarowej odwzorowującej przekształcenie n-wymiarowego wejścia w wyjście jednowymiarowe.
| \( v = f(\mathbf{e})\quad;\quad \forall e_i \in E_i\quad ;\quad \forall v\in V \) | (119) |
|---|
Przestrzenią sterowania będziemy określali hiperprzestrzeń rozpiętą w przestrzeni (n+m)-wymiarowej odwzorowującej operację przekształcenia n-wymiarowego wejścia w m-wymiarowe wyjście.
| \( \mathbf{v} = f(\mathbf{e})\quad;\quad \forall e_i \in E_i\quad ;\quad \forall v_i\in V_k \) | (120) |
|---|
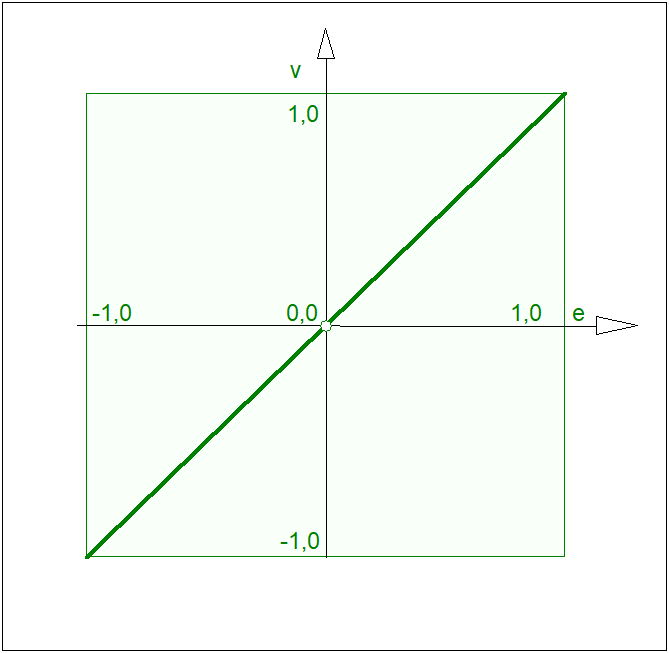
Ponieważ dla rozważanego przypadku regulatora P (n=m=1), to przestrzeń sterowania jest dwuwymiarowa (Rys. 30).
Jak łatwo zauważyć, funkcja sterowania regulatora skonstruowanego do tej pory jest funkcją liniową. A więc regulator posiada stałe wzmocnienie, którego wartość jest równa pochodnej funkcji sterowania względem sygnału wejściowego. Z Rys. 30 wynika, że wzmocnienie tego regulatora jest równe 1. Pojawia się pytanie czy w ogóle, a jeśli tak to w jaki sposób można kształtować wzmocnienie tego regulatora? Tę kwestię wyjaśnimy poniżej.
Jak łatwo zauważyć, w naszym przykładzie wartość wyjścia v wyznaczana jest z:
| \( v = \mu_{Ps}(v)-\mu_{Ns}(v)\quad;\quad \forall e\in E\quad ;\quad \forall v\in V \) | (121) |
|---|
gdzie: \( E \) i \( V \) ą odpowiednio przestrzeniami rozważań sygnału wejściowego i wyjściowego regulatora.
Ponieważ z reguł wnioskowania wynika, że:
| \( \mu_{Ps}(v)=\mu_{Pe}(e)\quad i\quad \mu_{Ns}(v)=\mu_{Ne}(e) \) | (122) |
|---|
to ostatecznie:
| \( v = \mu_{Pe}(e)-\mu_{Ne}(e)\quad;\quad \forall e\in E\quad ;\quad \forall v\in V \) | (123) |
|---|
Funkcje przynależności wartości \( P_e \) i \( N_e \) można zapisać w postaci funkcji liniowych będącymi kombinacjami liniowymi parametrów stałych: \( k_P \) , \( C_P \) , \( k_N \), \( C_N \):
| \( \mu_{Pe}(e)=k_{Pe}\cdot e + C_{Pe} \quad;\quad \mu_{Ne}(e)=k_{Ne}\cdot e+C_{Ne} \) | (124) |
|---|
stąd:
| \( v=(k_{Pe}-k_{Ne})\cdot e + (C_{Pe}-C_{Ne})\quad;\quad \forall e\in E\quad ;\quad \forall v\in V \) | (125) |
|---|
Z (125) wynika, że wzmocnienie regulatora można wyznaczyć z różnicy nachyleń funkcji przynależności <odchyłki regulacji>:
| \( k=(k_{P}-k_{N}) \) | (126) |
|---|
Podobnie, przesunięcie funkcji sterowania w kierunku osi sygnału wyjściowego v można wyznaczyć z różnicy przesunięć w tym kierunku obu funkcji przynależności <odchyłki regulacji>:
| \( C=(C_{P}-C_{N}) \) | (127) |
|---|
Ostatecznie otrzymujemy prawo sterowania w postaci funkcji liniowej:
| \( v=k\cdot e+C \) | (128) |
|---|
Zatem zmiana wzmocnienia regulatora rozmytego typu P sprowadza się do zadania kształtowaniu wartości współczynników nachylenia funkcji przynależności wejścia.
W naszym przykładzie \( k_{P_e} =0,5 \), \( k_{N_e} =-0,5 \), \( C_{P_e} =0,5 \), \( C_{N_e}=0,5 \) stąd zgodnie z wzorami (126) i (127) \( k =1 \); \( C =0 \).
Zaprojektować liniowy regulator rozmyty typu P o współczynniku wzmocnienia równym \( k_P=2 \).
Z zależności (126) otrzymujemy:
| \( k_p=k_{Pe}-k_{Ne}=2 \) | (129) |
|---|
Ponieważ równanie (125) jest równaniem z dwoma niewiadomymi to w celu jego rozwiązania przyjmiemy, że współczynniki kierunkowe obu funkcji przynależności zmiennej \ltodchyłka regulacji\gt będą identyczne co do wartości lecz będą miały znaki przeciwne, tzn. \( k_{Pe}=-k_{Ne}=k_e \). Po podstawieniu, z (129) wyznaczamy wartość \( k_e=1 \).
Dodatkowo założymy, aby funkcja sterowania przechodziła przez punkt o współrzędnych \( [0, 0] \) co zgodnie z (125) implikuje równość \( C_{Pe}=C_{Ne} \). Z (126) wynika, że wzmocnienie jest niezależne od doboru wartości stałych \( C_{Pe} \) i \( C_{Ne} \). W związku z tym przykładzie przyjmiemy arbitralnie \( C_{Pe}=C_{Ne}=0,5 \).
Na Rys. 35 przedstawiono wykres wartości funkcji przynależności sygnałów odchyłki regulacji i nastawiającego oraz funkcję sterowania. Natomiast w Tabeli 7 przedstawiono przebieg procesu wnioskowania.
| \( e \) | \( \mu_N(e) \) | \( \mu_P(e) \) | \( \mu_{N_s}(v) \) | \( \mu_{P_s}(v) \) | \( v \) |
|---|---|---|---|---|---|
| -1,00 | 1,00 | 0,00 | 1,00 | 0,00 | -1,00 |
| -0,75 | 1,00 | 0,00 | 1,00 | 0,00 | -1,00 |
| -0,50 | 1,00 | 0,00 | 1,00 | 0,00 | -1,00 |
| -0,25 | 0,75 | 0,25 | 0,75 | 0,25 | -0,50 |
| 0,00 | 0,50 | 0,50 | 0,50 | 0,50 | 0,00 |
| 0,25 | 0,25 | 0,75 | 0,25 | 0,75 | 0,50 |
| 0,50 | 0,00 | 1,00 | 0,00 | 1,00 | 0,00 |
| 0,75 | 0,00 | 1,00 | 0,00 | 1,00 | 0,00 |
| 1,00 | 0,00 | 1,00 | 0,00 | 1,00 | 0,00 |
| Wejście | Rozmywanie | Wnioskowanie | Wyjście | ||
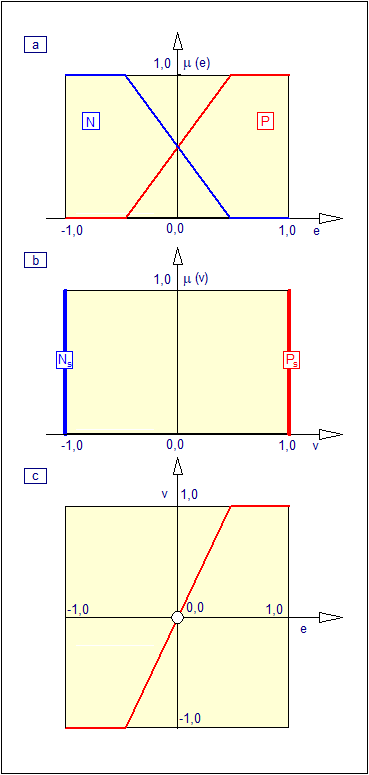
a) Funkcje przynależności wejścia \( e \)
b) Funkcje przynależności wyjścia \( v \)
c) Funkcja sterowania
