Podręcznik
Wstęp do logiki rozmytej
4. Przykłady regulatorów rozmytych
4.4. Rozmyty regulator typu PI
Transmitancja operatorowa liniowego regulatora PI dana jest równaniem:
| \( G(s)=k_p\left(1+\frac{1}{T_is}\right) \) | (130) |
|---|
gdzie: \( k_p \) – współczynnik wzmocnienia proporcjonalnego, \( T_i \) – stała czasowa całkowania.
Ponieważ w naszym przypadku:
| \( G(s)=\frac{V(s)}{E(s)} \) | (131) |
|---|
gdzie: \( E(s) \) i \( V(s) \) są odpowiednio transformatami Laplace'a wejścia i wyjścia regulatora. Po uwzględnieniu (130) i (131) otrzymujemy:
| \( V(s)=k_p\left(1+\frac{1}{T_is}\right)E(s) \) | (132) |
|---|
Stosując odwrotną transformatę Laplace'a, przy zerowych warunkach początkowych, otrzymujemy:
| \( v(t)=k_p\cdot e(t)+k_i\cdot \int_0^t e(t)dt \) | (133) |
|---|
gdzie: \( k_i=k_p/T_i \) - współczynnik członu całkującego.
Różniczkując obustronnie równanie (133) otrzymujemy:
| \( \frac{dv(t)}{dt}=k_p\cdot \frac{de(t)}{dt} + k_i\cdot e \) | (134) |
|---|
co prowadzi do wniosku, że cechą charakterystyczną regulatora PI jest to, że:
zmiana sygnału wyjściowego liniowego regulatora typu PI jest proporcjonalna zarówno do prędkości zmian odchyłki regulacji (akcja proporcjonalna) jak również do wartości samej odchyłki (akcja całkująca).
W systemach z czasem dyskretnym z okresem impulsowania ∆t równanie (134) przybiera postać następującego równania różnicowego:
| \( \Delta v=K_P \cdot \Delta e + K_I\cdot e \) | (135) |
|---|
gdzie: \(K_P=k_P \); \(K_I=k_I\Delta t \) ; \(\Delta t=const=1 \).
Równanie (135) stanowi podstawę do sformułowania reguł sterowania rozmytego regulatora typu PI. Reguły te można zapisać w postaci ogólnej:
| \( jezeli\; (e=E)\cap(\Delta e=\Delta E)\; to\; (\Delta v= \Delta V) \) | (136) |
|---|
gdzie: \( E \), \( \Delta E \), \( \Delta V \) - są odpowiednio zmiennymi lingwistycznymi <odchyłka regulacji>, <zmiana odchyłki regulacji> i <zmiana wyjścia regulatora>.
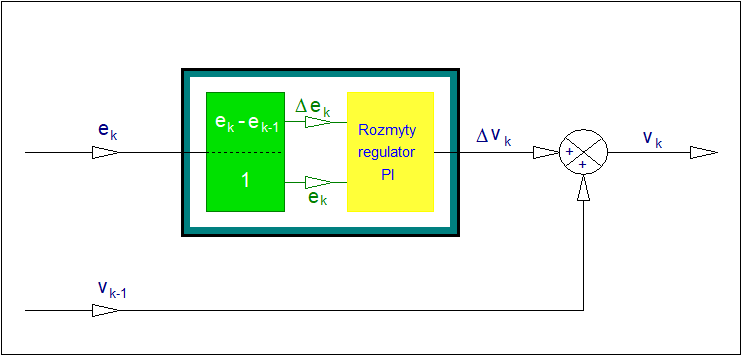
Wyjście dyskretnego regulatora PI (Rys. 34) w chwili k-tej jest sumą jego wyjścia \( v_{k-1} \) w chwili poprzedniej (k-1) i zmiany jego wyjścia \( \Delta v_{k-1} \) (korekty) dokonanej w chwili k- tej. Stąd:
| \( v_k= v_{k-1}+\Delta v_k \) | (137) |
|---|
Stąd:
| \( v=\sum_{i=1}^k\Delta v_i+v_0 \) | (138) |
|---|
gdzie: \( v_o \) – wartość początkowa (offset) wyjścia.
Podstawiając (135) do (138) otrzymujemy ostatecznie rekurencyjny wzór na wyjście rozmytego regulatora PI:
| \( v=\sum_{i=1}^k \left\{k_{P}(e_i-e_{i-1})+k_I\cdot e_i\right\}+v_0 \) | (139) |
|---|
Rozwiązanie: Zgodnie z procedurą syntezy układów rozmytych przedstawioną w podrozdziale 3.1, projekt rozmytego regulatora typu PI przeprowadzimy w sześciu krokach.
Krok 1 (formalny)
Załóżmy regulator typu PI o strukturze MISO. Wejściami regulatora będą: odchyłka regulacji \( e \) oraz prędkość tej odchyłki \( \Delta e \). W realizacjach praktycznych prędkości odchyłki regulacji w dyskretnej chwili k wyznaczymy z różnicy wartości odchyłki \( e \) w chwili k-tej i w chwili poprzedniej tj. \( e_{k-1} \).
| \( \Delta e_k=k_e \cdot (e_{k}-e_{k-1}) \) | (140) |
|---|
gdzie: \( k_e=1⁄{\Delta t}=const \); \( \Delta t \) - okres impulsowania.
Wyjściem regulatora jest zmiana sygnału nastawiającego \( \Delta v_k \). Przyporządkujmy zmiennej lingwistycznej <odchyłka regulacji> symbol \( e \), zmiennej lingwistycznej <prędkość odchyłki regulacji> symbol \( \Delta e \), zaś zmiennej lingwistycznej <zmiana sygnału wyjściowego> symbol \( \Delta v \). Załóżmy dalej, że zmiennej \( e \) przyporządkujemy dwie wartości <odchyłka ujemna> i <odchyłka dodatnia>. Wartościom tym nadano odpowiednio nazwy symboliczne: \( N_e \) i \( P_e \). W podobny sposób zmiennej <prędkość odchyłki regulacji> \( \Delta e \) przyporządkowano wartości <ujemna wartość prędkości odchyłki regulacji> i <dodatnia wartość prędkości odchyłki regulacjigt. Wartościom tym nadano odpowiednio nazwy symboliczne: \( N_{\Delta e} \) i \( P_{\Delta e} \). Zmiennej lingwistycznej \( v \) przyporządkowano wartości <zmniejsz sterowanie>, <pozostaw sterowanie bez zmian> i <zwiększ sterowanie>. Wartościom tym nadano odpowiednio nazwy symboliczne \( N_{\Delta v} \), \( Z_{\Delta v} \) i \( P_{\Delta v} \).
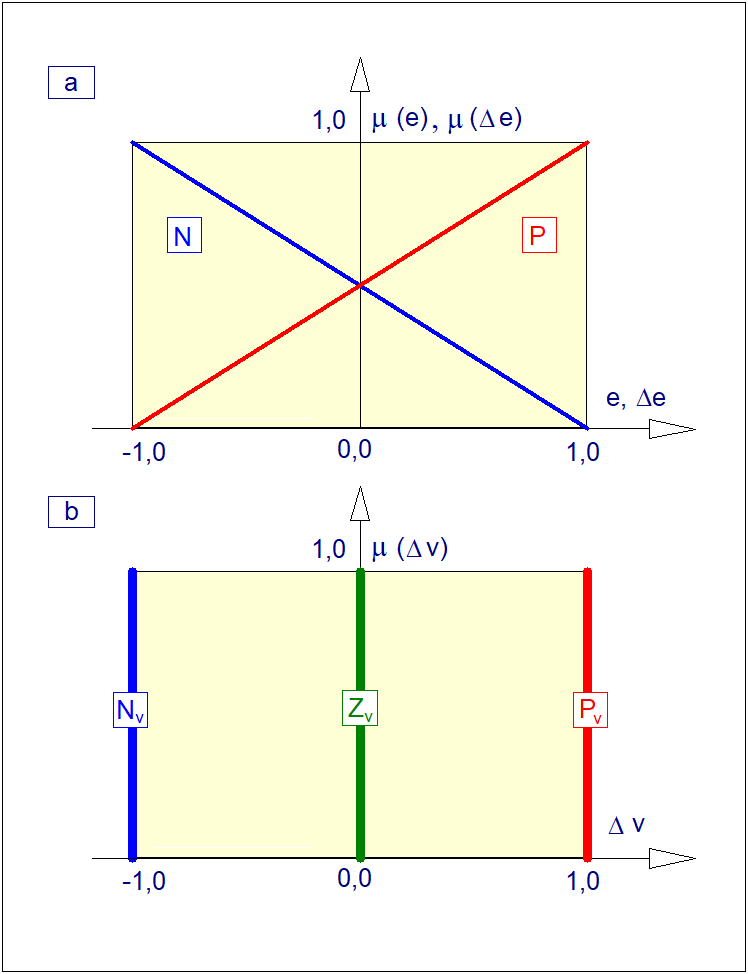
Projekt zbiorów rozmytych wejścia i wyjścia przedstawimy graficznie na Rys. 35. W tym przypadku wyjście rozmyte zaprojektowano w postaci singletonów, co jak już wspomniano wcześniej znakomicie upraszcza i przyśpiesza proces wyostrzania.
Krok 3 (projekt bazy reguł)
Posiłkując się znajomością ogólnej reguły warunkowej (136) regulatora rozmytego typu PI; mając na uwadze kształt funkcji przynależności jak na Rys. 35, zbudujemy zupełną bazę reguł modelu regulatora. W tym przypadku mamy do czynienia z układem rozmytym o dwóch wejściach (i=2) i jednym wyjściu (k=1). Obu wejściom przyporządkowano odpowiednio: \( n_1=2 \) i \( n_2=2 \) zbiorów rozmytych. Stąd liczba reguł bazy zupełnej zgodnie ze wzorem (102) wynosi: \( r=1\cdot (2\cdot 2)=4 \).
| Reguła | \( \Delta e \) | \( e \) | \( \Delta y \) |
|---|---|---|---|
| 1 | \( N_{\Delta e} \) | \( N_e \) | \( N_{\Delta v} \) |
| 2 | \( N_{\Delta e} \) | \( P_e \) | \( Z_{\Delta v} \) |
| 3 | \( P_{\Delta e} \) | \( N_e \) | \( Z_{\Delta v} \) |
| 2 | \( P_{\Delta e} \) | \( P_e \) | \( P_{\Delta v} \) |
a) Funkcje przynależności wejścia \( e \) i \( \Delta e \)
b) Funkcje przynależności wyjścia \(\Delta v \)
Krok 4, 5, 6 (wyznaczenie wartości rozmytej wejść, wyznaczenie wartości rozmytej wyjścia, wyznaczenie wartości wyjścia ostrego)
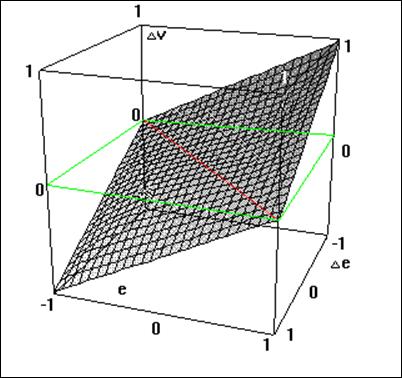
Na podstawie znajomości wartości wejść ostrych, znajomości zbiorów rozmytych wejść (krok 2) oraz znajomości tabeli reguł (krok 3) wyznaczymy wyjścia ostre regulatora PI stosując implikację Mamdaniego (82), agregację wniosków rozmytych zgodnych z formułą sumy mnogościowej (106) oraz wyostrzanie metodę środka ciężkości COG (111). Ze względu na singletonowy kształt funkcji przynależności przyporządkowanych do wyjścia regulatora, wynik wyostrzania metodą COG jest w tym przypadku równoważny wynikom uzyskiwanym metodami COS i HM. W tabeli 10 przedstawiono przebieg procesu wnioskowania, a na Rys. (36 przedstawiono powierzchnię sterowania regulatora. Powierzchnia sterowania, która ma kształt płaszczyzny jest charakterystyczna dla liniowych regulatorów PI. Konstrukcja nieliniowego regulatora PI możliwa jest np. przez zmianę kształtu i położenia funkcji przynależności wejścia.
| Reguła | 1 | 2 | 3 | 4 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| \( \Delta e \) | \( e \) | \( \mu_N(\Delta e) \) | \( \mu_P(\Delta e) \) | \( \mu_N(e) \) | \( \mu_P(\Delta e) \) | \( \mu_N(\Delta v) \) | \( \mu_Z(\Delta v) \) | \( \mu_Z(\Delta v) \) | \( \mu_P(\Delta v) \) | \( \Delta v \) |
| -1,00 | -1,00 | 1,00 | 0,00 | 1,00 | 0,00 | 1,00 | 0,00 | 0,00 | 0,00 | -1,00 |
| -0,50 | 0,75 | 0,25 | 1,00 | 0,00 | 0,75 | 0,00 | 0,25 | 0,00 | -1,00 | |
| 0,00 | 0,50 | 0,50 | 1,00 | 0,00 | 0,50 | 0,00 | 0,50 | 0,00 | -0,50 | |
| 0,50 | 0,25 | 0,75 | 1,00 | 0,00 | 0,25 | 0,00 | 0,75 | 0,00 | -0,25 | |
| 1,00 | 0,00 | 1,00 | 1,00 | 0,00 | 0,00 | 0,00 | 1,00 | 0,00 | 0,00 | |
| -1,00 | -0,50 | 1,00 | 0,00 | 0,75 | 0,25 | 0,75 | 0,25 | 0,00 | 0,00 | -0,75 |
| -0,50 | 0,75 | 0,25 | 0,75 | 0,25 | 0,75 | 0,25 | 0,25 | 0,25 | -0,40 | |
| 0,00 | 0,50 | 0,50 | 0,75 | 0,25 | 0,50 | 0,25 | 0,50 | 0,25 | -0,20 | |
| 0,50 | 0,25 | 0,75 | 0,75 | 0,25 | 0,25 | 0,25 | 0,75 | 0,25 | 0,00 | |
| 1,00 | 0,00 | 1,00 | 0,75 | 0,25 | 0,00 | 0,00 | 0,75 | 0,25 | 0,25 | |
| -1,00 | 0,00 | 1,00 | 0,00 | 0,50 | 0,50 | 0,50 | 0,50 | 0,00 | 0,00 | -0,50 |
| -0,50 | 0,75 | 0,25 | 0,50 | 0,50 | 0,50 | 0,50 | 0,25 | 0,25 | -0,20 | |
| 0,00 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,50 | 0,00 | |
| 0,50 | 0,25 | 0,75 | 0,50 | 0,50 | 0,25 | 0,20 | 0,50 | 0,50 | 0,20 | |
| 1,00 | 0,00 | 1,00 | 0,50 | 0,50 | 0,00 | 0,00 | 0,50 | 0,50 | 0,50 | |
| -1,00 | 0,50 | 1,00 | 0,00 | 0,25 | 0,75 | 0,05 | 0,75 | 0,00 | 0,00 | -0,25 |
| -0,50 | 0,75 | 0,25 | 0,25 | 0,75 | 0,25 | 0,75 | 0,25 | 0,25 | 0,00 | |
| 0,00 | 0,50 | 0,50 | 0,25 | 0,75 | 0,25 | 0,50 | 0,25 | 0,50 | 0,20 | |
| 0,50 | 0,25 | 0,75 | 0,25 | 0,75 | 0,25 | 0,25 | 0,25 | 0,75 | 0,75 | |
| 1,00 | 0,00 | 1,00 | 0,25 | 0,75 | 0,00 | 0,00 | 0,25 | 0,75 | 0,75 | |
| -1,00 | 1,00 | 1,00 | 0,00 | 0,00 | 1,00 | 0,00 | 1,00 | 0,00 | 0,00 | 0,00 |
| -0,50 | 0,75 | 0,25 | 0,00 | 1,00 | 0,00 | 0,75 | 0,00 | 0,25 | 0,25 | |
| 0,00 | 0,50 | 0,50 | 0,00 | 1,00 | 0,00 | 0,50 | 0,00 | 0,50 | 0,50 | |
| 0,50 | 0,25 | 0,75 | 0,00 | 1,00 | 0,00 | 0,25 | 0,00 | 0,75 | 0,75 | |
| 1,00 | 0,00 | 1,00 | 0,00 | 1,00 | 0,00 | 0,00 | 0,00 | 1,00 | 1,00 | |
| Wejście | Rozmywanie | Wnioskowanie | Wyjście | |||||||
Redukcja regulatora rozmytego typu PI do regulatora P
Zaprojektujemy tabelę reguł rozmytego regulatora typu PI o trzech wartościach zmiennej \( e \), trzech wartościach zmiennej \( \Delta e \) i trzech wartościach zmiennej \( \Delta v \) jak na Rys. 37. Odchyłce regulacji \( e \) przyporządkujemy trzy wartości <odchyłka ujemna>, <odchyłka zerowa> i <odchyłka dodatnia>. Wartościom tym nadano nazwy symboliczne: \( N_e \), \( Z_e \) i \( P_e \). W podobny sposób zmiennej <zmiana odchyłki regulacji> \( \Delta e \) przyporządkowano wartości <ujemna zmiana odchyłki regulacji>, <brak zmiany odchyłki regulacji> i <dodatnia zmiana odchyłki regulacji>. Wartościom tym nadano także nazwy symboliczne: \( N_{\Delta e} \), \( Z_{\Delta e} \) i \( P_{\Delta e} \). Zmiennej \( \Delta v \) przyporządkowano wartości <zmniejsz sterowanie> , <sterowanie bez zmian> i <zwiększ sterowanie>. Wartościom tym nadano odpowiednio nazwy symboliczne \( N_{\Delta v} \), \( Z_{\Delta v} \) i \( P_{\Delta v} \).
Rozwiązanie: Na podstawie ogólnej reguły warunkowej (136) dla regulatora rozmytego typu PI, mając na uwadze kształt funkcji przynależności jak na Rys. 37, oraz wnioski z rozważań przeprowadzonych w tym rozdziale, zbudujemy bazę zupełną regulatora. W tym przypadku mamy do czynienia z układem o dwóch wejściach (i=2). Obu wejściom przyporządkowano odpowiednio: \( n_1=3 \) i \( n_2=3 \) zbiorów rozmytych. Stąd liczba reguł bazy zupełnej zgodnie ze wzorem (102) wynosi: \( r=1\cdot (3\cdot 3)=9 \). Tabelę sterowań tego regulatora przedstawiono w Tabeli 11.
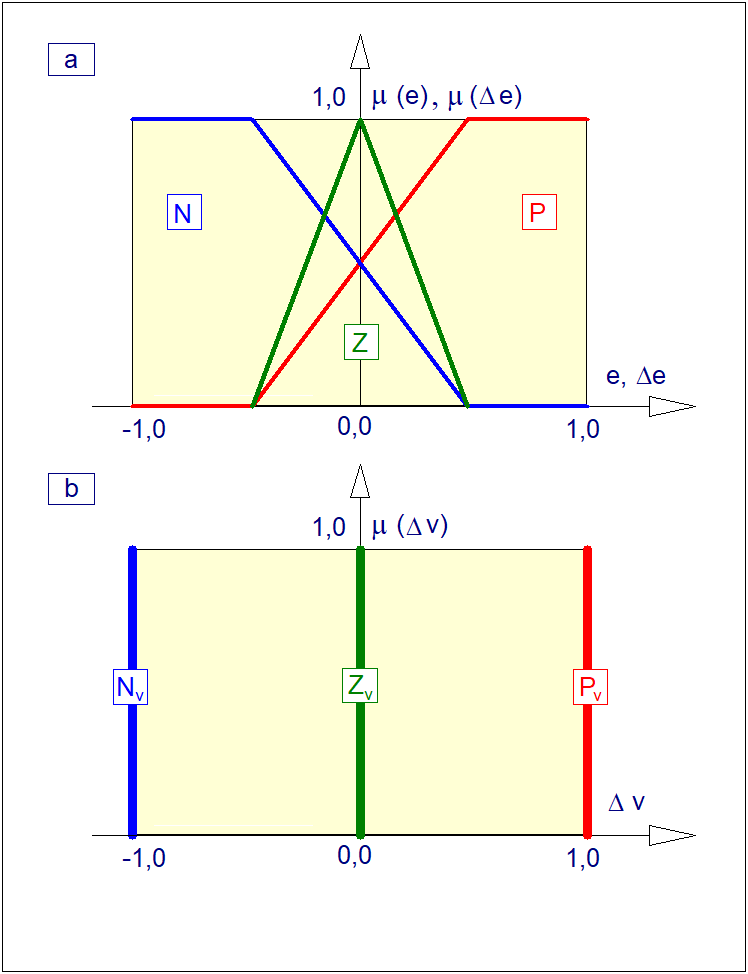
a) Funkcje przynależności wejść \( e \) i \( \Delta e \)
b) Funkcje przynależności wyjścia \( \Delta v \)
| Regulator rozmyty typu PI |
\( e \) | |||
|---|---|---|---|---|
| \( N_e \) | \( Z_e \) | \( P_e \) | ||
| \( \Delta e \) | \( N_{\Delta e} \) | \( N_{\Delta v} \) | \( N_{\Delta v} \) | \( Z_{\Delta v} \) |
| \( Z_{\Delta e} \) | \( N_{\Delta v} \) | \( Z_{\Delta v} \) | \( P_{\Delta v} \) | |
| \( P_{\Delta e} \) | \( Z_{\Delta v} \) | \( P_{\Delta v} \) | \( P_{\Delta v} \) | |
Zwróćmy uwagę, że jeśli w równaniu (133) dokonamy podstawienia \( e=0 \), to regulator PI ulegnie redukcji do regulatora typu P. Wówczas zmiana sygnału wyjściowego będzie wprost proporcjonalna do zmiany odchyłki regulacji.
| \( \Delta v=K_p \cdot \Delta e \) | (141) |
|---|
A zatem \( {\Delta v}/{\Delta e}=const \) i \( \lim_{t \to \infty } \frac{\Delta v}{\Delta e}=v/e \) co jest charakterystyczną cechą regulatora o działaniu proporcjonalnym.
Technicznie redukcja regulatora PI do regulatora typu P polega na wyeliminowaniu z tabeli sterowań 11, dwóch kolumn, dotyczą wartości niezerowych rozmytych odchyłek regulacji. Postać zredukowanej tabeli sterowań dla regulatora typu P przedstawiono w Tabeli 12.
| Regulator rozmyty typu PI |
\( e \) | |||
|---|---|---|---|---|
| - | \( Z_e \) | - | ||
| \( \Delta e \) | \( N_{\Delta e} \) | - | \( N_{\Delta v} \) | - |
| \( Z_{\Delta e} \) | - | \( Z_{\Delta v} \) | - | |
| \( P_{\Delta e} \) | - | \( P_{\Delta v} \) | - | |
Zwróćmy także uwagę, że przekształcenie klasycznego regulatora PI do regulatora typu P może być dokonane przez podstawienie \( k_i=k_p/T_i =0 \) we wzorze (134). Technicznie można tego dokonać albo przez maksymalizację stałej czasowej całkowania \( T_i \), albo przez wyeliminowanie akcji całkującej z wzoru (134). Pierwszy sposób realizowany był w regulatorach analogowych starszych typów, zaś drugi jest obecnie stosowany powszechnie we współczesnych regulatorach implementowanych w technice cyfrowej.
