Podręcznik
Wstęp do logiki rozmytej
4. Przykłady regulatorów rozmytych
4.5. Rozmyty regulator typu PD
Transmitancja operatorowa idealnego liniowego regulatora PD dana jest równaniem:
| \( G(s)=k_p\left(1+T_{d}s\right) \) | (142) |
|---|
Ponieważ
| \( G(s)=\frac{V(s)}{E(s)} \) | (143) |
|---|
gdzie: \( E(s) \) i \( V(s) \) są odpowiednio transformatami Laplace'a wejścia i wyjścia regulatora.
Po uwzględnieniu (142) i (143) otrzymujemy:
| \( V(s)=k_p\left(1+T_{d }s\right)E(s) \) | (144) |
|---|
Stosując odwrotną transformatę Laplace'a, przy zerowych warunkach początkowych, otrzymujemy:
| \( v(t)=k_p\cdot e(t)+k_d\cdot\frac{de(t)}{dt} \) | (145) |
|---|
gdzie: \( k_d=k_p\cdot T_d \) - współczynnik członu różniczkującego.
Jak wynika ze wzoru (145), cechą charakterystyczną regulatora PD jest to, że: jego sygnał wyjściowy jest proporcjonalny zarówno do odchyłki regulacji (akcja proporcjonalna) jak i jej prędkości (akcja różniczkująca).
W systemach z czasem dyskretnym z okresem impulsowania \( \Delta t \) równanie (145) przybiera postać następującego równania różnicowego:
| \( \frac{dv(t)}{dt}=k_p\cdot \frac{de(t)}{dt} + k_i\cdot e \) | (146) |
|---|
gdzie: \( K_p=k_p \); \( K_d=k_d/\Delta t \); \( \Delta t=const \).
Równanie (146) stanowi podstawę do sformułowania reguł sterowania rozmytego regulatora typu PD. Reguły te można zapisać w postaci ogólnej:
| \( v=K_P \cdot e + K_D\cdot \Delta e \) | (147) |
|---|
gdzie: \( E \), \( \Delta E \), \( V \) - są odpowiednio zmiennymi lingwistycznymi <odchyłka regulacji>, <zmiana odchyłki regulacji> i <wyjście regulatora>.
Projekt rozmytego regulatora typu PD.
Rozwiązanie: Zgodnie z procedurą przedstawioną w tym rozdziale syntezę bazy reguł rozmytego regulatora typu PD przeprowadzimy w trzech krokach.
Krok 1 (formalny)
Załóżmy regulator typu PD o strukturze MISO. Wejściami regulatora będą: odchyłka regulacji \( e \) i prędkość tej odchyłki \( \Delta e \). Prędkość odchyłki \( \Delta e \) w dyskretnej chwili k wyznaczymy z różnicy wartości odchyłki \( e \) w chwili k-tej i w chwili ją poprzedzającej tj. \( e_{k-1} \). Wyjściem regulatora jest sygnał sterujący (nastawiający) regulatora \( v \). Przyporządkujmy odchyłce regulacji zmiennej lingwistycznej <odchyłka regulacji> symbol \( e \), zmiennej lingwistycznej <prędkość odchyłki regulacji> symbol \( \Delta e \), zaś zmiennej lingwistycznej <wyjście regulatora>" symbol \( v \). Załóżmy dalej, że zmiennej \( e \) przyporządkujemy trzy wartości <odchyłka ujemna>, <odchyłka zerowa> i <odchyłka dodatnia>. Wartościom tym nadano nazwy symboliczne: \( N_e \) , \( Z_e \) i \( P_e \). W podobny sposób zmiennej <prędkość odchyłki regulacji> \( \Delta e \) przyporządkowano wartości <ujemna prędkość odchyłki regulacji>, <zerowa prędkość odchyłki regulacji> i <dodatnia prędkość odchyłki regulacji>. Wartościom tym nadano nazwy symboliczne: \( N_{\Delta e} \), \( Z_{\Delta e} \) i \( P_{\Delta e} \). Zmiennej \( v \) przyporządkowano wartości <ujemne wyjście regulatora>, <zerowe wyjście regulatora> i <dodatnie wyjście regulatora>. Wartościom tym nadano odpowiednio nazwy symboliczne: \( N_v \), \( Z_v \) i \( P_v \).
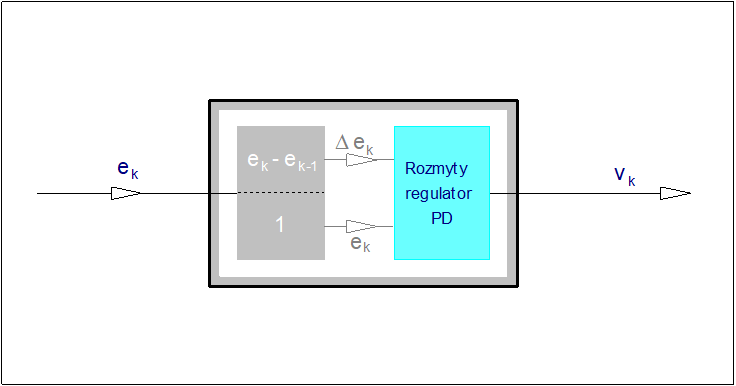
Założymy, że kształty zbiorów rozmytych wejść i wyjścia regulatora będą identyczne jak dla regulatora PI (Rys. 35), jedynie z tą jedynie różnicą, że w miejsce symbolu \( \Delta v \) na tym rysunku zostanie podstawiony symbol \( v \).
Krok 3 (projekt bazy reguł)
Posiłkując się znajomością ogólnej reguły warunkowej (147) regulatora rozmytego typu PD oraz mając na uwadze kształt funkcji przynależności jak na Rys. 35, zbudujemy zupełną bazę reguł modelu regulatora rozmytego. W przypadku rozważanego regulatora typu PD mamy do czynienia z układem o dwóch wejściach (i=2) i jednym wyjściu. Obu wejściom przyporządkowano odpowiednio: \( n_1=3 \) i \( n_2=3 \) zbiorów rozmytych. Stąd, liczba reguł bazy zupełnej zgodnie ze wzorem (102).
wynosi: \( r=1\cdot (3\cdot 3)=9 \). Tabelę reguł dla tego regulatora przedstawiono w Tab. 13.| Regulator rozmyty typu PD |
\( e \) | |||
|---|---|---|---|---|
| \( N_e \) | \( Z_e \) | \( P_e \) | ||
| \( \Delta e \) | \( N_{\Delta e} \) | \( N_{\Delta v} \) | \( N_{\Delta v} \) | \( Z_{\Delta v} \) |
| \( Z_{\Delta e} \) | \( N_{\Delta v} \) | \( Z_{\Delta v} \) | \( P_{\Delta v} \) | |
| \( P_{\Delta e} \) | \( Z_{\Delta v} \) | \( P_{\Delta v} \) | \( P_{\Delta v} \) | |
Dość zaskakujące jest to, że jest ona identyczna jak dla regulatora typu PI.
Nasuwa to praktyczny wniosek, że proces wnioskowania i wyniki tego procesu będą identyczne jak w przypadku regulatora PI (Tab. 10). Dotyczy to oczywiście także identycznej powierzchni sterowania przedstawionej na Rys. 36. Wniosek ten ma duże znaczenie praktyczne. W przypadku implementacji różnych algorytmów sterowania wystarcza bowiem zaimplementować jedną ogólną procedurę regulatora rozmytego. Wywołanie takiej procedury z różnymi zestawami parametrów formalnych generuje różne typy regulatorów (P, PI, PD).
Z podobieństwa tabel sterowania regulatorów PI i PD można próbować wyprowadzić wniosek o uniwersalności reguł sterowania, co niewątpliwie ma duże znaczenie praktyczne. Tak jest w istocie. W praktyce dostępne są uniwersalne (tzw. szablonowe) bazy reguł, które można implementować do modelowania całej klasy pokrewnych układów rozmytych. Stosowane są one często jako bazy wyjściowe w procesie iteracyjnym polegającym na strojeniu reguł bazy, liczby, kształtu i położenia funkcji przynależności. Zagadnienie strojenia układów rozmytych wychodzi jednak poza zakres tego skryptu.
Powstaje w związku z tym pytanie, na czym polega różnica pomiędzy implementacją regulatorów typu PI i PD. Otóż różnica polega nie tyle na różnicy w metodzie prowadzeniu procesu wnioskowania rozmytego, co na różnicy struktur obu regulatorów, co zilustrowano na Rys. 34 i Rys. 38.
Zwróćmy także uwagę, że jeśli w równaniu (145) dokonamy podstawienia \( \Delta e=0 \), to regulator PD ulegnie przekształceniu do regulatora typu P. Wówczas sygnał wyjściowy będzie wprost proporcjonalny wyłącznie do odchyłki regulacji co jest charakterystyczną cechą regulatora o działaniu proporcjonalnym.
| \( jezeli\; (e=E)\cap(\Delta e=\Delta E)\; to\; (v=V) \) | (148) |
|---|
Technicznie redukcja regulatora PD do regulatora typu P polega na wyeliminowaniu z Tab. 13 wierszy dotyczą wartości niezerowych rozmytych prędkości odchyłek regulacji. Postać zredukowanej tabeli sterowań dla regulatora typu P przedstawiono w Tab. 14.
| Regulator rozmyty typu PD |
\( e \) | |||
|---|---|---|---|---|
| \( N_e \) | \( Z_e \) | \( P_e \) | ||
| \( \Delta e \) | \( N_{\Delta e} \) | |||
| \( Z_{\Delta e} \) | \( N_{v} \) | \( Z_{v} \) | \( P_{v} \) | |
| \( P_{\Delta e} \) | ||||
Zwróćmy także uwagę, że przekształcenie klasycznego regulatora PI do regulatora typu P może być dokonane przez podstawienie \( k_d=k_p\cdot T_d=0 \) we wzorze (145). Technicznie można tego dokonać albo przez przyrównanie stałej czasowej różniczkowania \( T_d \) do zera albo przez wyeliminowanie akcji różniczkującej z wzoru (145). Pierwszy sposób realizowany był w regulatorach analogowych starszych typów, zaś drugi jest obecnie stosowany powszechnie we współczesnych regulatorach implementowanych w technice cyfrowej.
