Podręcznik
Wstęp do logiki rozmytej
6. Przykłady zastosowań logiki rozmytej
6.1. Regulator mikroprocesorowy EFTRONIK XF typ U496
Źródło: Dokumentacja techniczno-ruchowa DTR-U496-01, wydanie I, Zakład Systemów Automatyki MERA-PNEFAL S.A., 1997, s. 96.
Czterokanałowy regulator mikroprocesorowy EFTRONIK XF typ U496 produkcji Zakładu Systemów Automatyki MERA-PNEFAL S.A.
Podstawową zaletą regulatora EFTRONIK XF jest możliwość zastosowania liniowych algorytmów regulatorów PID do sterowania procesów nieliniowych. W przypadku procesów nieliniowych, przy znacznych zmianach wartości zadanej SP lub znacznej amplitudzie zakłóceń, regulatory realizujące konwencjonalne algorytmy PID mogą być nieskuteczne w tym sensie, że nie zapewniają uzyskania założonych kryteriów jakości regulacji lub wręcz prowadzą do utraty stabilności.
Jeśli właściwości dynamiczne lub/i parametry regulownego procesu zależą od wartości zadanej, to dla każdej jej wartości (punktu pracy) i niewielkiego otoczenia tego punktu można dobrać lokalny liniowy regulator PID zapewniający spełnienie wymaganych kryteriów jakości regulacji. Można też pokusić się o projekt regulatora PID o parametrach będącymi ciągłymi bądź nieciągłymi funkcjami wartości zadanej. W praktyce można w tym celu posłużyć się zbiorem kilku lub kilkunastu zestawów nastaw (\( k_p \), \( T_i \),\( T_d \)) regulatorów lokalnych zaprojektowanych dla różnych punktów pracy.
Taką właściwość posiada regulator EFTRONIK XF. Umożliwia on zapis i zapamiętanie łącznie do 10 zestawów lokalnych nastaw PID w każdym z jego czterech kanałów regulacyjnych.
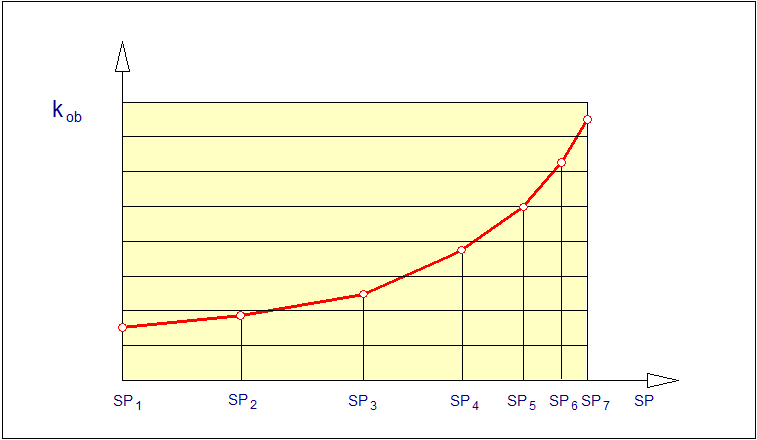
Przykładową charakterystykę nieliniowego obiektu regulacji, w którym współczynnik wzmocnienia obiektu \( k_{ob} \) jest funkcją punktu pracy przedstawiono na Rys. 41. Na tym rysunku przedstawiono również sposób określania wartości punktów węzłowych \( SP_i \), dla których wyznaczane są zestawy parametrów lokalnych regulatorów PID.
Sposób ten jest następujący. Najpierw zakres zmian wartości zadanej \( SP \) dzielony jest na obszarów (partycji) wyznaczonych dyskretnymi punktami \( SP_i \). Wartości \( SP_i \) dobierane są w taki sposób, aby różnicom wartości zadanych \( SP_i-SP_{i-1} \) odpowiadały w przybliżeniu takie same zmiany współczynnika wzmocnienia obiektu \( k_{ob} \). Jak można zauważyć, ten sposób wyznaczania punktów \( SP_i \) pozwala w istocie na dokonanie liniowej aproksymacji odcinkowej funkcji \( k_{ob}=f(SP) \).
Przypuśćmy, że dla małych odchyleń wielkości regulowanej od wartości \( SP_1 \) uzyskano doświadczalnie zbiór nastaw \( (k_p^{(1)},T_i^{(1)},T_d^{(1)}) \) lokalnego regulatora \( PID^{(1)} \). Podobnie, dla wartości zadanej \( SP_2 \) uzyskano zbiór nastaw \( (k_p^{(2)},T_i^{(2)},T_d^{(2)}) \), itd. Przy zachowaniu odpowiedniej procedury postępowania uzyskane zestawy nastaw mogą być zapisane do pamięci regulatora w postaci odpowiednich tablic.
W przypadku realizacji sterowania rozmytego, w każdym kroku sterowania, a więc dla każdej chwilowej wartości wielkości regulowanej PV następuje wyznaczenie chwilowych nastaw regulatora PID. W tym celu tworzone są w regulatorze w sposób automatyczny zbiory rozmyte o trójkątnych funkcjach przynależności (jak na rys. 42). Liczba zbiorów rozmytych jest równa liczbie zestawów parametrów regulatorów lokalnych wprowadzonych do pamięci kanału regulacyjnego regulatora. Funkcje przynależności tych zbiorów są tak skonstruowane, że każdej wartości regulowanej (mierzonej) \( PV_i \) odpowiadają co najwyżej dwa punkty przecięcia \( \mu_1(PV_i) \) i \( \mu_2(PV_i) \) jak pokazano na Rys. 42.
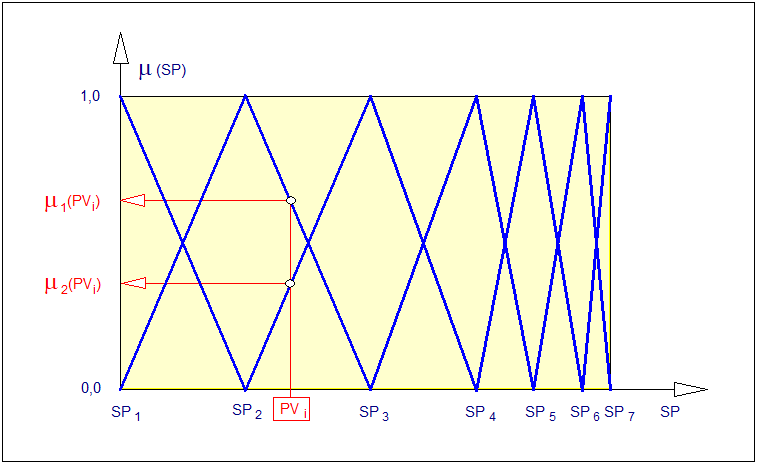
Jeśli zatem wartość sygnału wyjściowego obiektu w i-tej chwili czasowej jest równa \( PV_i \) (tzn. dynamiczny punkt pracy jest równy \( PV_i \)) to odpowiadają mu wartości funkcji przynależności \( \mu_1(PV_i) \) i \( \mu_2(PV_i) \), przy założeniu, że przestrzenie rozważań dla \( SP \) i \( PV \) są tożsame. Z Rys. 42 wynika, że:
| \( \mu_1(PV_i)=\frac{(SP_3-PV_i)}{(SP_3-SP_2)} \) | (166) |
|---|
| \( \mu_2(PV_i)=1-\mu_1(PV_i) \) | (167) |
|---|
Stąd wyznaczane są wartości \( k_p(PV_i) \), \( T_i(PV_i) \) i \( T_d(PV_i) \) z zależności:
| \( k_p(PV_i)=\mu_1(PV_i)\cdot k_{p2}+\mu_2(PV_i)\cdot k_{p3} \) | (168) |
|---|
| \( T_i(PV_i)=\left(\mu_1(PV_i)\cdot k_{p2}\cdot T_{i2} +\mu_2(PV_i)\cdot k_{p3}\cdot T_{i3}\right)/kp_2(PV_i) \) | (169) |
|---|
| \( T_d(PV_i)=0,25\cdot T_i(PV_i)\cdot W_{PID} \) | (170) |
|---|
gdzie: \( k_{p2} \), \( k_{p3} \) - współczynniki wzmocnienia w punktach pracy \( SP_2 \) i \( SP_3 \),
\( T_{i2} \), \( T_{i3} \) - czasy zdwojenia (całkowania)w punktach pracy \( SP_2 \) i \( SP_3 \),
\( PV_i \) - rzeczywisty punkt pracy obiektu regulacji,
\( W_{PID} \) - współczynnik przyjmujący wartość 1 dla regulatora PID i wartość 0 dla regulatora PI.
Spróbujemy wykazać, że ten prosty algorytm rozmytego doboru parametrów regulatora PID jest równoważny wnioskowaniu Takagi-Sugeno. Dla skoncentrowania uwagi przypatrzmy się zależności (166).
Ponieważ \( \mu_1(PV_i) \) (patrz Rys. 42) jest dopełnieniem \( \mu_2(PV_i) \) to ich suma arytmetyczna zgodnie z (49) jest równa 1. Zatem wyrażenie (166) można traktować jako średnią ważoną wartości \( k_{p2} \) i \( k_{p3} \). Współczynnikami wagowymi są tutaj wartości funkcji przynależności \( \mu_1(PV_i) \) i \( \mu_2(PV_i) \). Możemy zatem sądzić, że zależność (166) może być jedną z postaci rozwinięcia wzoru (156). Skoro tak, to dokonamy rekonstrukcji zbioru reguł regulatora pozwalających na wyznaczenie współczynnika wzmocnienia \( k_p \) w postaci:
| \( \begin{array}{c} R^{(1)}:if\; (PV\:\:is\:\:SP_1)\; then\; k_{p}=k_{p1}\\ R^{(2)}:if\; (PV\:\:is\:\:SP_2)\; then\; k_{p}=k_{p2}\\ \dots\dots\\ R^{(n)}:if\; (PV\:\:is\:\:SP_n)\; then\; k_{p}=k_{pn} \end{array} \) | (171) |
|---|
W podobny sposób wyznaczane są: stała czasowa całkowania \( T_i \) oraz stała czasowa różniczkowania \( T_d \).
Zatem regulator EFTRONIK XF należy traktować jako regulator PID, w którym dobór jego parametrów jest zależny od wartości regulowanej i jest realizowany automatycznie z wykorzystaniem wnioskowania aproksymatora rozmytego Sugeno-Takagi.
